Optimalisatieberekeningen met de oplosser
De oplosser kan worden ingezet bij het oplossen van optimalisatievraagstukken met twee of meer onbekende variabelen. Bij winstmaximalisatie is meestal sprake van meerdere variabelen en meerdere beperkende voorwaarden.
Werkbladen in deze Excelsheet
|
Werkblad Winstmaximalisatie voor optimalisatie |
Bekijk screenshot van dit werkblad |
|
Werkblad Winstmaximalisatie na optimalisatie |
Bekijk screenshot van dit werkblad |
|
Werkblad Antwoordrapport bij winstmaximalisatie |
Bekijk screenshot van dit werkblad |
|
Werkblad Winstmaximalisatie na optimalisatie plus urenrestrictie |
Bekijk screenshot van dit werkblad |
Gebruiksinstructie
Doel van deze tool
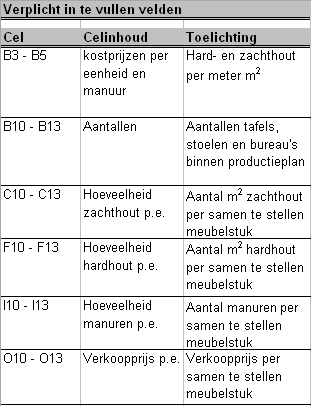
We gaan uit van een meubelbedrijf dat zowel tafels, stoelen, bureaus als kasten maakt. Voor de productie hiervan is het volgende nodig aan materiaal- en arbeidsuren:
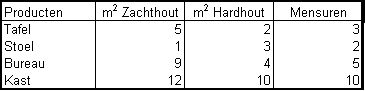
De kostprijzen zijn:

en aansluitend bedragen de verkoopprijzen:

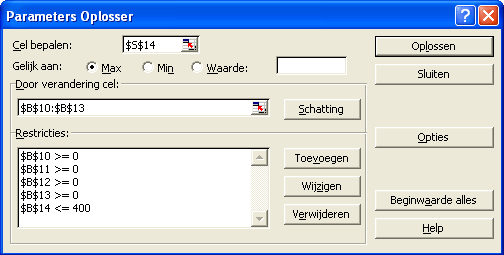
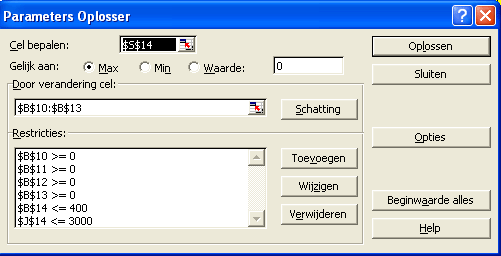
Het meubelbedrijf streeft naar winstmaximalisatie, maar ziet zich daarbij beperkt in de productiecapaciteit die maximaal 400 eenheden bedraagt.
Personeelsmanagement

Heeft u ook een verantwoordelijkheid in personeelsmanagement? Kijk dan ook op HR Praktijk voor zekerheid over wetten en regels!
Gerelateerde Excelsheets
-
 Annuïteitentafel
Annuïteitentafel
-
 Berekening aantal annuïteiten met gegeven bedrag en...
Berekening aantal annuïteiten met gegeven bedrag en...
-
 Berekening annuïteit op meerjarige basis
Berekening annuïteit op meerjarige basis
-
 Berekening contante waarde één kapitaal met gebroken...
Berekening contante waarde één kapitaal met gebroken...
-
 Berekening contante waarde één kapitaal met...
Berekening contante waarde één kapitaal met...
-
 Berekening contante waarde eindige discontinue reeks...
Berekening contante waarde eindige discontinue reeks...
-
 Berekening contante waarde eindige reeksen met...
Berekening contante waarde eindige reeksen met...
-
 Berekening contante waarde oneindige groeireeks
Berekening contante waarde oneindige groeireeks
-
 Berekening contante waarde reeks betalingen plus één...
Berekening contante waarde reeks betalingen plus één...
-
 Berekening contante waarde reeks gelijke betalingen
Berekening contante waarde reeks gelijke betalingen
-
 Berekening contante waarde regelmatige betalingsreeksen
Berekening contante waarde regelmatige betalingsreeksen
-
 Berekening contante waarde van eindige reeksen met...
Berekening contante waarde van eindige reeksen met...
-
 Berekening eindwaarde één kapitaal bij wisselende...
Berekening eindwaarde één kapitaal bij wisselende...
-
 Berekening eindwaarde één kapitaal met jaarlijkse...
Berekening eindwaarde één kapitaal met jaarlijkse...
-
 Berekening eindwaarde één kapitaal met wisselende...
Berekening eindwaarde één kapitaal met wisselende...
-
 Berekening eindwaarde één kapitaal plus regelmatige...
Berekening eindwaarde één kapitaal plus regelmatige...
-
 Berekening eindwaarde eindige discontinue reeks...
Berekening eindwaarde eindige discontinue reeks...
-
 Berekening eindwaarde eindige reeksen met wisselende...
Berekening eindwaarde eindige reeksen met wisselende...
-
 Berekening eindwaarde van eindige reeksen met...
Berekening eindwaarde van eindige reeksen met...
-
 Berekening jaarlijkse annuïteit
Berekening jaarlijkse annuïteit
-
 Berekening veelvoorkomende renteconversies
Berekening veelvoorkomende renteconversies
-
 Berekeningen eindwaarde regelmatige betalingsreeksen
Berekeningen eindwaarde regelmatige betalingsreeksen
-
 Converteren van reeksen betalingen
Converteren van reeksen betalingen
-
 Functie RENTE
Functie RENTE
-
 Functies Effect.Rente en Nominale.Rente
Functies Effect.Rente en Nominale.Rente
-
 Intresttafel berekenen van contante waarde van reeks...
Intresttafel berekenen van contante waarde van reeks...
-
 Intresttafel voor berekenen eindwaarde van reeks...
Intresttafel voor berekenen eindwaarde van reeks...
-
 Leasing
Leasing
-
 Minimalisatie van de distributiekosten
Minimalisatie van de distributiekosten
-
 Optimaal vastzetten van overtollige middelen
Optimaal vastzetten van overtollige middelen
-
 Optimalisatieberekeningen met de oplosser
Optimalisatieberekeningen met de oplosser
-
 Renteconversie omzetten naar gelijkwaardige procenten
Renteconversie omzetten naar gelijkwaardige procenten
-
 Spaarplanning
Spaarplanning
-
 Tafel voor het berekenen van de constante waarde van...
Tafel voor het berekenen van de constante waarde van...
-
 Tafel voor het berekenen van de eindwaarde van één...
Tafel voor het berekenen van de eindwaarde van één...
-
 Vijf basisfuncties: BET, HW, NPER, RENTE, TW
Vijf basisfuncties: BET, HW, NPER, RENTE, TW
-
 Winstmaximalisatie van de distributiekosten
Winstmaximalisatie van de distributiekosten