Berekeningen eindwaarde regelmatige betalingsreeksen
In deze werkbladen wordt de eindwaarde berekend van een reeks gelijke bedragen pre- of postnumerando óf minus een correctie.
Bij het berekenen van de eindwaarde van een reeks betalingen is het volgende van belang:
- Elk van de betalingen noemt men een termijn, terwijl het tijdsverloop tussen twee opeenvolgende termijnen als periode wordt aangeduid.
- Vervallen de betalingen aan het begin van de perioden, dan spreken we van prenumerando betalingen; vervallen ze daarentegen aan het eind van de perioden, dan spreken we van postnumerando betalingen.
Werkbladen in deze Excelsheet
|
Werkblad Berekeningen eindwaarde van reeks gelijke bedragen – prenumerando reeks |
Bekijk screenshot van dit werkblad |
|
Werkblad Berekeningen eindwaarde van reeks gelijke bedragen – postnumerando reeks |
Bekijk screenshot van dit werkblad |
|
Werkblad Berekeningen eindwaarde van reeks gelijke bedragen minus correctie |
Bekijk screenshot van dit werkblad |
Gebruiksinstructie
Introductie
Bij de eindwaardeberekening van één kapitaal zagen we dat de intrest bij de hoofdsom werd opgeteld tot het moment van uitbetaling. Hetzelfde geldt voor de eindwaarde van een regelmatige reeks betalingen. Bij de eindwaarde van een reeks betalingen is het volgende van belang:
- elk van de betalingen noemt men een termijn, terwijl het tijdsverloop tussen twee opeenvolgende termijnen als periode wordt aangeduid;
- vervallen de betalingen aan het begin van de perioden, dan spreken we van prenumerando betalingen; vervallen ze daarentegen aan het eind van de perioden, dan spreken we van postnumerando betalingen.
Bij eindwaardeberekeningen van een regelmatige reeks betalingen rekenen we met de algemene formule voor een afdalende of opklimmende meetkundige reeks. Indien we rekenen vanuit het heden naar het eindwaardemoment, luidt de formule in termen van een afdalende meetkundige reeks:

waarbij:
EW = de eindwaarde van de betalingsreeks;
a = de eerste term van de meetkundige reeks;
r = de reden van de meetkundige reeks;
n = het aantal termen van de meetkundige reeks.
In de financiële literatuur wordt hiervoor ook wel de volgende 'kleine s'-schrijfwijze aangetroffen:
EW = termijnbedrag * sn-p
met:
p = de samengestelde intrestvoet;
n = het aantal perioden.
Voorbeeld 1
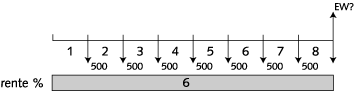
Bereken de eindwaarde van een dadelijk ingaande prenumerando betalingsreeks van acht termijnen, elk groot € 500, per het einde van het achtste jaar. De intrestvoet bedraagt 6% jaarlijks.
Schematisch volgens het kasstroomdiagram:
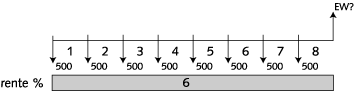
Oplossing:
Van elk der betalingen van € 500 moeten we de eindwaarde berekenen per het einde van het achtste jaar:
500 * (1,068 + 1,067 + ... + 1,062 + 1,06)
Toepassing van de formule voor de afdalende reeks geeft:
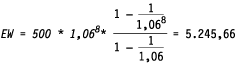
Voorbeeld 2
Bereken de eindwaarde op 31 december 2020 van een prenumerando betalingsreeks groot € 300, waarvan de eerste termijn vervalt op 1 januari 2008 en de laatste op 1 januari 2015. De intrestvoet is 5% per jaar.
Schematisch volgens het kasstroomdiagram:

Hierbij passen we de formule voor de afdalende reeks 'dubbel' toe : één maal over de totale periode (dertien termijnen) minus een 'correctie' voor de laatste vijf termijnen, omdat de reeks na acht perioden eindigt.
Personeelsmanagement

Heeft u ook een verantwoordelijkheid in personeelsmanagement? Kijk dan ook op HR Praktijk voor zekerheid over wetten en regels!
Gerelateerde Excelsheets
-
 Annuïteitentafel
Annuïteitentafel
-
 Berekening aantal annuïteiten met gegeven bedrag en...
Berekening aantal annuïteiten met gegeven bedrag en...
-
 Berekening annuïteit op meerjarige basis
Berekening annuïteit op meerjarige basis
-
 Berekening contante waarde één kapitaal met gebroken...
Berekening contante waarde één kapitaal met gebroken...
-
 Berekening contante waarde één kapitaal met...
Berekening contante waarde één kapitaal met...
-
 Berekening contante waarde eindige discontinue reeks...
Berekening contante waarde eindige discontinue reeks...
-
 Berekening contante waarde eindige reeksen met...
Berekening contante waarde eindige reeksen met...
-
 Berekening contante waarde oneindige groeireeks
Berekening contante waarde oneindige groeireeks
-
 Berekening contante waarde reeks betalingen plus één...
Berekening contante waarde reeks betalingen plus één...
-
 Berekening contante waarde reeks gelijke betalingen
Berekening contante waarde reeks gelijke betalingen
-
 Berekening contante waarde regelmatige betalingsreeksen
Berekening contante waarde regelmatige betalingsreeksen
-
 Berekening contante waarde van eindige reeksen met...
Berekening contante waarde van eindige reeksen met...
-
 Berekening eindwaarde één kapitaal bij wisselende...
Berekening eindwaarde één kapitaal bij wisselende...
-
 Berekening eindwaarde één kapitaal met jaarlijkse...
Berekening eindwaarde één kapitaal met jaarlijkse...
-
 Berekening eindwaarde één kapitaal met wisselende...
Berekening eindwaarde één kapitaal met wisselende...
-
 Berekening eindwaarde één kapitaal plus regelmatige...
Berekening eindwaarde één kapitaal plus regelmatige...
-
 Berekening eindwaarde eindige discontinue reeks...
Berekening eindwaarde eindige discontinue reeks...
-
 Berekening eindwaarde eindige reeksen met wisselende...
Berekening eindwaarde eindige reeksen met wisselende...
-
 Berekening eindwaarde van eindige reeksen met...
Berekening eindwaarde van eindige reeksen met...
-
 Berekening jaarlijkse annuïteit
Berekening jaarlijkse annuïteit
-
 Berekening veelvoorkomende renteconversies
Berekening veelvoorkomende renteconversies
-
 Berekeningen eindwaarde regelmatige betalingsreeksen
Berekeningen eindwaarde regelmatige betalingsreeksen
-
 Converteren van reeksen betalingen
Converteren van reeksen betalingen
-
 Functie RENTE
Functie RENTE
-
 Functies Effect.Rente en Nominale.Rente
Functies Effect.Rente en Nominale.Rente
-
 Intresttafel berekenen van contante waarde van reeks...
Intresttafel berekenen van contante waarde van reeks...
-
 Intresttafel voor berekenen eindwaarde van reeks...
Intresttafel voor berekenen eindwaarde van reeks...
-
 Leasing
Leasing
-
 Minimalisatie van de distributiekosten
Minimalisatie van de distributiekosten
-
 Optimaal vastzetten van overtollige middelen
Optimaal vastzetten van overtollige middelen
-
 Optimalisatieberekeningen met de oplosser
Optimalisatieberekeningen met de oplosser
-
 Renteconversie omzetten naar gelijkwaardige procenten
Renteconversie omzetten naar gelijkwaardige procenten
-
 Spaarplanning
Spaarplanning
-
 Tafel voor het berekenen van de constante waarde van...
Tafel voor het berekenen van de constante waarde van...
-
 Tafel voor het berekenen van de eindwaarde van één...
Tafel voor het berekenen van de eindwaarde van één...
-
 Vijf basisfuncties: BET, HW, NPER, RENTE, TW
Vijf basisfuncties: BET, HW, NPER, RENTE, TW
-
 Winstmaximalisatie van de distributiekosten
Winstmaximalisatie van de distributiekosten