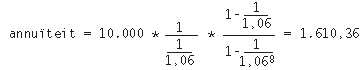Berekening jaarlijkse annuïteit
Onder een annuïteit van een geldlening wordt verstaan een vaste periodieke betaling bestaande uit een aflossingsbestanddeel en een intrestbestanddeel. In dit werkblad wordt de jaarlijkse annuïteit berekend.
Werkbladen in deze Excelsheet
|
Werkblad Berekening jaarlijkse annuïteit |
Bekijk screenshot van dit werkblad |
Gebruiksinstructie
Introductie
Onder een annuïteit van een geldlening verstaan we een vaste periodieke betaling bestaande uit:
- een aflossingsbestanddeel;
- een intrestbestanddeel.
In het wat verdere verleden gebruikte men bij de berekening lijvige annuïteitentafels. Deze tafels gaven de annuïteit van één waarde-eenheid, bij een gegeven looptijd en een gegeven intrestvoet van een lening. In een annuïteitentafel vinden we bijvoorbeeld dat per waarde-eenheid kapitaal de 8-jarige annuïteit 0,16103594 bedraagt bij een intrestvoet van 6%. Bij een lening van 10.000 waarde-eenheden betekent dit jaarlijks 10.000 x 0,16103594 = 1.610,36 aan aflossing en intrest.
Hierna bekijken we eerst de algemene rekenregels die van toepassing zijn op annuïteitenberekeningen. Vervolgens gaan we naar Excel en laten we zien dat annuïteitenberekeningen betrekkelijk eenvoudig zijn op te lossen met de basisfuncties, met name de functie BET(rente;aantal-termijnen;hw;tw;type_getal).
Rekenregels bij annuïteiten
a. De hoogte van annuïteiten (= het termijnbedrag)
De contante waarde van de annuïteiten gedurende de looptijd van een lening moet gelijk zijn aan de hoogte van de lening. Volgens de algemene formule van een dalende meetkundige reeks geldt:
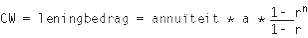
of in enigszins herschreven vorm:

met:
a = de eerste term van de meetkundige reeks;
r = de reden van de meetkundige reeks;
n = het aantal termen van de meetkundige reeks.
b. De hoogte van de rente- en aflossingsbestanddelen
Een annuïteit is altijd opgebouwd uit een rente- en een aflossingsbestanddeel. Daarbij geldt voor alle perioden 1 tot en met n:
annuïteit = afl.1 + rente1 = afl.2 + rente2 = ... = afl.n + renten
De som van het rente- en aflossingsdeel (= de annuïteit) is in de tijd een constante.
c. De hoogte van het rente- en het aflossingsbestanddeel in periode 1
De hoogte van het rentebestanddeel in periode 1 bedraagt:
rente1 = i * leningbedrag
met:
i = de intrestvoet van de geldlening.
De hoogte van het aflossingsbestanddeel in periode 1 bedraagt dan:
afl.1 = annuïteit – rente1
d. De hoogte van het rente- en het aflossingsbestanddeel in alle volgende perioden
De hoogte van het aflossingsbestanddeel in periode n bedraagt bijvoorbeeld:
afl.n = afl.n – 1 * (1 + i)
Dit is dus een per periode met de intrestvoet stijgende aflossingsreeks.
De hoogte van het rentebestanddeel in periode n bedraagt dan het verschil:
renten = annuïteit – afl.n
Dit is dus een in de tijd dalende rentereeks.
Personeelsmanagement

Heeft u ook een verantwoordelijkheid in personeelsmanagement? Kijk dan ook op HR Praktijk voor zekerheid over wetten en regels!
Gerelateerde Excelsheets
-
 Annuïteitentafel
Annuïteitentafel
-
 Berekening aantal annuïteiten met gegeven bedrag en...
Berekening aantal annuïteiten met gegeven bedrag en...
-
 Berekening annuïteit op meerjarige basis
Berekening annuïteit op meerjarige basis
-
 Berekening contante waarde één kapitaal met gebroken...
Berekening contante waarde één kapitaal met gebroken...
-
 Berekening contante waarde één kapitaal met...
Berekening contante waarde één kapitaal met...
-
 Berekening contante waarde eindige discontinue reeks...
Berekening contante waarde eindige discontinue reeks...
-
 Berekening contante waarde eindige reeksen met...
Berekening contante waarde eindige reeksen met...
-
 Berekening contante waarde oneindige groeireeks
Berekening contante waarde oneindige groeireeks
-
 Berekening contante waarde reeks betalingen plus één...
Berekening contante waarde reeks betalingen plus één...
-
 Berekening contante waarde reeks gelijke betalingen
Berekening contante waarde reeks gelijke betalingen
-
 Berekening contante waarde regelmatige betalingsreeksen
Berekening contante waarde regelmatige betalingsreeksen
-
 Berekening contante waarde van eindige reeksen met...
Berekening contante waarde van eindige reeksen met...
-
 Berekening eindwaarde één kapitaal bij wisselende...
Berekening eindwaarde één kapitaal bij wisselende...
-
 Berekening eindwaarde één kapitaal met jaarlijkse...
Berekening eindwaarde één kapitaal met jaarlijkse...
-
 Berekening eindwaarde één kapitaal met wisselende...
Berekening eindwaarde één kapitaal met wisselende...
-
 Berekening eindwaarde één kapitaal plus regelmatige...
Berekening eindwaarde één kapitaal plus regelmatige...
-
 Berekening eindwaarde eindige discontinue reeks...
Berekening eindwaarde eindige discontinue reeks...
-
 Berekening eindwaarde eindige reeksen met wisselende...
Berekening eindwaarde eindige reeksen met wisselende...
-
 Berekening eindwaarde van eindige reeksen met...
Berekening eindwaarde van eindige reeksen met...
-
 Berekening jaarlijkse annuïteit
Berekening jaarlijkse annuïteit
-
 Berekening veelvoorkomende renteconversies
Berekening veelvoorkomende renteconversies
-
 Berekeningen eindwaarde regelmatige betalingsreeksen
Berekeningen eindwaarde regelmatige betalingsreeksen
-
 Converteren van reeksen betalingen
Converteren van reeksen betalingen
-
 Functie RENTE
Functie RENTE
-
 Functies Effect.Rente en Nominale.Rente
Functies Effect.Rente en Nominale.Rente
-
 Intresttafel berekenen van contante waarde van reeks...
Intresttafel berekenen van contante waarde van reeks...
-
 Intresttafel voor berekenen eindwaarde van reeks...
Intresttafel voor berekenen eindwaarde van reeks...
-
 Leasing
Leasing
-
 Minimalisatie van de distributiekosten
Minimalisatie van de distributiekosten
-
 Optimaal vastzetten van overtollige middelen
Optimaal vastzetten van overtollige middelen
-
 Optimalisatieberekeningen met de oplosser
Optimalisatieberekeningen met de oplosser
-
 Renteconversie omzetten naar gelijkwaardige procenten
Renteconversie omzetten naar gelijkwaardige procenten
-
 Spaarplanning
Spaarplanning
-
 Tafel voor het berekenen van de constante waarde van...
Tafel voor het berekenen van de constante waarde van...
-
 Tafel voor het berekenen van de eindwaarde van één...
Tafel voor het berekenen van de eindwaarde van één...
-
 Vijf basisfuncties: BET, HW, NPER, RENTE, TW
Vijf basisfuncties: BET, HW, NPER, RENTE, TW
-
 Winstmaximalisatie van de distributiekosten
Winstmaximalisatie van de distributiekosten