Risicometing bij verschillende beleggingsvormen: variantie (VAR) en standaarddeviatie (SD) als maatstaven
We bekijken hier de relatie tussen rendement en risico voor investeringen in het algemeen en voor beleggingen in het bijzonder. Het rendement dat beleggers of investeerders wensen, hangt nauw samen met de risicograad van de projecten of ondernemingen waarin ze beleggen of investeren. Bij de risicometing van de verschillende beleggingsvormen gebruiken we de variantie (VAR) en de standaarddeviatie (SD) als maatstaven.
Werkbladen in deze Excelsheet
|
Werkblad Spreiding bij aandelen met gemiddeld risico |
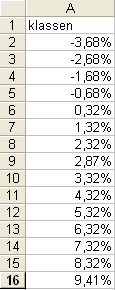
Bekijk screenshot van dit werkblad |
|
Werkblad Spreiding bij aandelen met hoog risico |
Bekijk screenshot van dit werkblad |
|
Werkblad Spreiding bij bedrijfsobligaties |
Bekijk screenshot van dit werkblad |
|
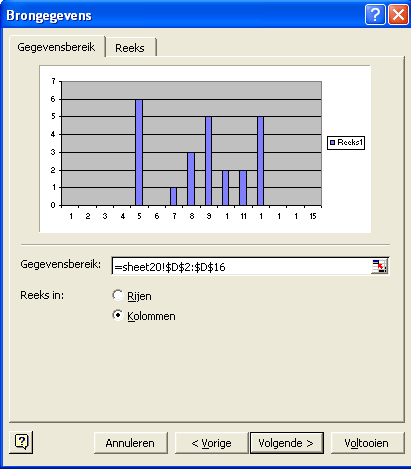
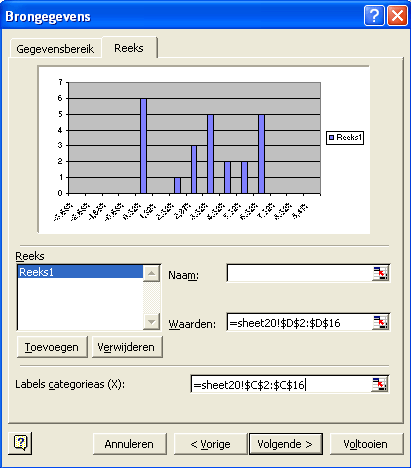
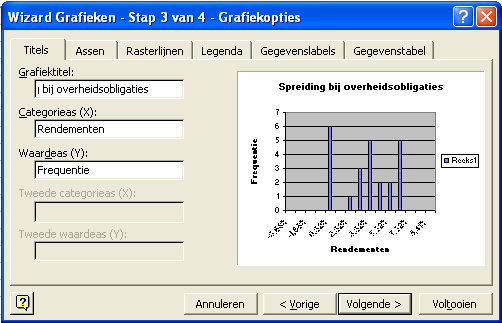
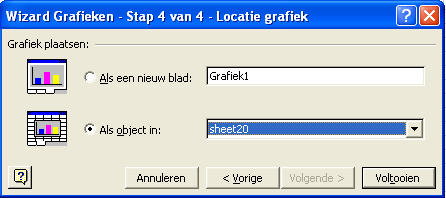
Werkblad Spreiding bij overheidsobligaties |
Bekijk screenshot van dit werkblad |
|
Werkblad Spreiding bij schatkistpapier |
Bekijk screenshot van dit werkblad |
Gebruiksinstructie
Doel van deze tool
We zien in het werkblad Rendement en risico van diverse beleggingen dat bij aandelen met een hoog risicoprofiel het hoogste gemiddeld rendement wordt behaald over een periode van 25 jaar. Daartegenover staat dat ook de variantie van de behaalde rendementen het hoogst is in deze categorie. Het omgekeerde geldt voor schatkistpapier, waar zowel het gemiddeld behaalde rendement als de variantie het laagst scoort.
De variantie (Var) van een steekproef met n waarnemingen (ook wel aangeduid als σ2x) berekenen we daarbij als volgt:
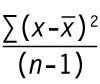
waarbij X de verschillende individuele rendementen weergeeft en 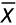 het rekenkundig gemiddelde over alle rendementen. De parameter n geeft het aantal waarnemingen in de steekproef weer.
het rekenkundig gemiddelde over alle rendementen. De parameter n geeft het aantal waarnemingen in de steekproef weer.
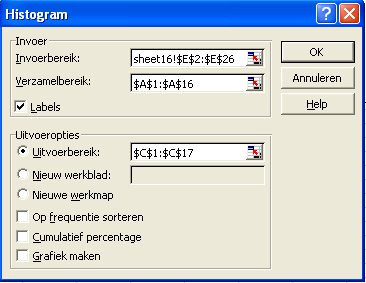
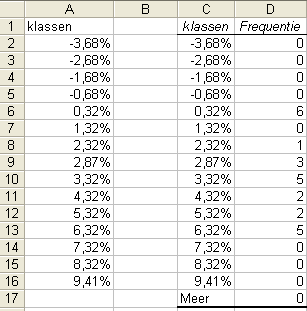
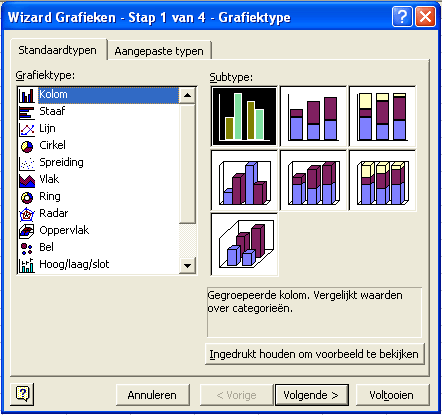
Met behulp van de ingebouwde Excel-functie VAR(getal 1;getal 2;...) hebben we in rij 32 van het werkblad Rendement en risico van diverse beleggingen de variantie berekend bij de verschillende beleggingscategorieën. Hierop aansluitend is in rij 33, met behulp van de ingebouwde Excel-functie STDEV(getal 1;getal 2;...) de standaarddeviatie (ook wel aangeduid als σx) bepaald als zijnde de wortel van de variantie:
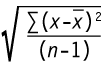
De standaarddeviatie (SD) hebben we nodig om de spreiding rond het rekenkundig gemiddelde te bepalen, uitgaande van een zogenaamde normale verdeling. Bij een normale verdeling ziet de kansverdeling van waarnemingen er ideaaltypisch als volgt uit:
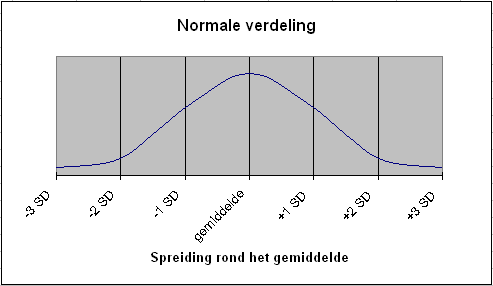
Hierop sluit de volgende verdeling aan:
- tussen de grenzen van -1 SD en +1 SD bevindt zich 68,26 procent van de waarnemingen;
- tussen de grenzen van -2 SD en +2 SD bevindt zich 95,44 procent van de waarnemingen;
- tussen de grenzen van -3 SD en +3 SD bevindt zich 99,84 procent van de waarnemingen.
Personeelsmanagement

Heeft u ook een verantwoordelijkheid in personeelsmanagement? Kijk dan ook op HR Praktijk voor zekerheid over wetten en regels!
Gerelateerde Excelsheets
-
 Covariantie, correlatie en regressie bij diversificatie
Covariantie, correlatie en regressie bij diversificatie
-
 Een optie op de oliemarkt als casus
Een optie op de oliemarkt als casus
-
 Een rendementsrisicomatrix in Excel
Een rendementsrisicomatrix in Excel
-
 Een vastrentende lening door een swap variabel maken
Een vastrentende lening door een swap variabel maken
-
 Forward bij een verwachte rentedaling
Forward bij een verwachte rentedaling
-
 Forward bij een verwachte rentestijging
Forward bij een verwachte rentestijging
-
 Futures
Futures
-
 Gevoeligheidratio's bij de prijsvorming van opties
Gevoeligheidratio's bij de prijsvorming van opties
-
 Het Black-Scholes-Merton-model
Het Black-Scholes-Merton-model
-
 Het Black-Scholes-model
Het Black-Scholes-model
-
 Historische en impliciete volatiliteit
Historische en impliciete volatiliteit
-
 Koop call-opties
Koop call-opties
-
 Koop putopties
Koop putopties
-
 On-balance hedging tegen renterisico's
On-balance hedging tegen renterisico's
-
 Optieprijzen berekenen met het binomiale model
Optieprijzen berekenen met het binomiale model
-
 Opties Algemeen
Opties Algemeen
-
 Opties op (staats)obligaties. beschermende werking...
Opties op (staats)obligaties. beschermende werking...
-
 Opties op (staats)obligaties: callopties in...
Opties op (staats)obligaties: callopties in...
-
 Overige afschermende rente-instrumenten: caps,...
Overige afschermende rente-instrumenten: caps,...
-
 Rendement en risico van investeringen en beleggingen
Rendement en risico van investeringen en beleggingen
-
 Renterisico's meten: yieldcurve en duration
Renterisico's meten: yieldcurve en duration
-
 Risicometing bij verschillende beleggingsvormen:...
Risicometing bij verschillende beleggingsvormen:...
-
 Valutaswaps
Valutaswaps
-
 Valutatermijntransacties
Valutatermijntransacties
-
 Van een variabel rentende belegging door een swap...
Van een variabel rentende belegging door een swap...