Het Black-Scholes-model
Het Black-Scholes-model wordt in het algemeen gebruikt om de (theoretische) waarde van Europese opties te berekenen. De formule vergemakkelijkt bovendien de prijsbepaling van optiecontracten die niet op de beurs worden verhandeld en waarvoor geen officiële marktnotering beschikbaar is.
Werkbladen in deze Excelsheet
|
Werkblad Black-Scholes-prijsberekening voor call- en putopties |
Bekijk screenshot van dit werkblad |
Gebruiksinstructie
Introductie
In 1973 verscheen het duo Black & Scholes met het (nog steeds) baanbrekende artikel 'The pricing of Options and Corporate Liabilities', waarin ze de prijsvorming van opties in directe relatie brengen met de factoren tijd en onzekerheid.
In het artikel stellen ze dat de prijsvorming van opties afhankelijk is van:
- de volatiliteit ofwel de mate waarmee fluctuaties optreden in de tijd. Opties waarvan de onderliggende waarden veel volatiliteit vertonen, hebben een hogere risicograad en daarmee een hogere prijs of risicopremie. De standaarddeviatie is de maatstaf waarmee het risico wordt gemeten;
- de uitoefenprijs waartegen de koper het optierecht kan uitoefenen;
- de lengte van de periode waarover het recht geldt, tot het moment dat de optie expireert, over het algemeen geldt: hoe langer de (resterende) periode, hoe hoger het risico en hoe hoger de optiepremie;
- de intrestvoet.
Het Black-Scholes-model wordt in het algemeen gebruikt om de (theoretische) waarde van Europese opties te berekenen. De formule vergemakkelijkt bovendien de prijsbepaling van optiecontracten die niet op de beurs worden verhandeld en waarvoor geen officiële marktnotering beschikbaar is. Dit is belangrijk aangezien het volume van onderhands ('over the counter') verhandelde contracten dat van de op de beurs verhandelde opties ruim overtreft. Voor beursgenoteerde opties biedt de formule een betrouwbaar hulpmiddel om onder- of overgewaardeerde opties te identificeren.
Het model is gebaseerd op een aantal aannames:
- De volatiliteit en de intrestvoet worden tot aan het expiratiemoment constant verondersteld.
- Toekomstige prijsontwikkeling vindt plaats onafhankelijk van prijsontwikkelingen in het verleden.
- Er wordt geen rekening gehouden met mogelijk bijkomende heffingen, toeslagen en belastingen.
- De waarschijnlijkheidsverdeling van de (relatieve) prijsveranderingen in de tijd is 'lognormaal' verdeeld (dat wil zeggen gemiddelde en afwijkingen worden gemeten aan de hand van een natuurlijk-logaritmische (In) schaal). Deze verdeling levert geringere afwijkingen van het gemiddelde en minder extreme waarden op.
- In het oorspronkelijke model wordt geen rekening gehouden met (mogelijke) dividenduitkeringen (in het door Merton aangepaste model is dit wel het geval).
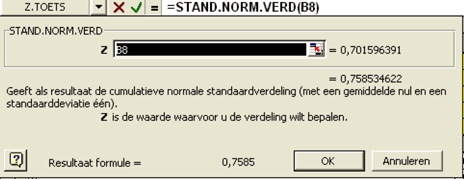
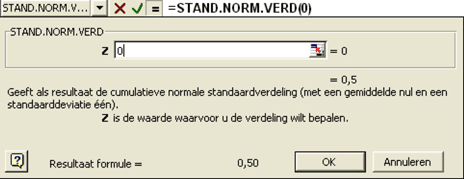
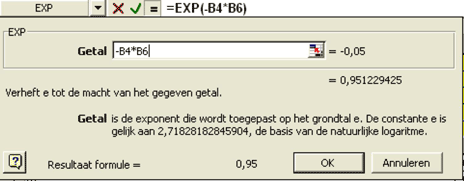
De mathematische uitwerking van het model ziet er op het eerste gezicht indrukwekkend uit, maar is feitelijk niet meer dan een hulpmiddel om op een gemakkelijke manier met behulp van slechts vijf invoervariabelen tot de waarde van een optie te komen.
Personeelsmanagement

Heeft u ook een verantwoordelijkheid in personeelsmanagement? Kijk dan ook op HR Praktijk voor zekerheid over wetten en regels!
Gerelateerde Excelsheets
-
 Covariantie, correlatie en regressie bij diversificatie
Covariantie, correlatie en regressie bij diversificatie
-
 Een optie op de oliemarkt als casus
Een optie op de oliemarkt als casus
-
 Een rendementsrisicomatrix in Excel
Een rendementsrisicomatrix in Excel
-
 Een vastrentende lening door een swap variabel maken
Een vastrentende lening door een swap variabel maken
-
 Forward bij een verwachte rentedaling
Forward bij een verwachte rentedaling
-
 Forward bij een verwachte rentestijging
Forward bij een verwachte rentestijging
-
 Futures
Futures
-
 Gevoeligheidratio's bij de prijsvorming van opties
Gevoeligheidratio's bij de prijsvorming van opties
-
 Het Black-Scholes-Merton-model
Het Black-Scholes-Merton-model
-
 Het Black-Scholes-model
Het Black-Scholes-model
-
 Historische en impliciete volatiliteit
Historische en impliciete volatiliteit
-
 Koop call-opties
Koop call-opties
-
 Koop putopties
Koop putopties
-
 On-balance hedging tegen renterisico's
On-balance hedging tegen renterisico's
-
 Optieprijzen berekenen met het binomiale model
Optieprijzen berekenen met het binomiale model
-
 Opties Algemeen
Opties Algemeen
-
 Opties op (staats)obligaties. beschermende werking...
Opties op (staats)obligaties. beschermende werking...
-
 Opties op (staats)obligaties: callopties in...
Opties op (staats)obligaties: callopties in...
-
 Overige afschermende rente-instrumenten: caps,...
Overige afschermende rente-instrumenten: caps,...
-
 Rendement en risico van investeringen en beleggingen
Rendement en risico van investeringen en beleggingen
-
 Renterisico's meten: yieldcurve en duration
Renterisico's meten: yieldcurve en duration
-
 Risicometing bij verschillende beleggingsvormen:...
Risicometing bij verschillende beleggingsvormen:...
-
 Valutaswaps
Valutaswaps
-
 Valutatermijntransacties
Valutatermijntransacties
-
 Van een variabel rentende belegging door een swap...
Van een variabel rentende belegging door een swap...