Het Black-Scholes-Merton-model
Het Black-Scholes-model wordt in het algemeen gebruikt om de (theoretische) waarde van Europese opties te berekenen. In het oorspronkelijke Black-Scholes-model wordt geen rekening gehouden met mogelijke dividenduitkeringen. Merton heeft hiervoor het oorspronkelijke model op verschillende plaatsen uitgebreid met de parameter q: het jaarlijks (gemiddelde) dividenduitkeringspercentage.
Werkbladen in deze Excelsheet
|
Werkblad Black-Scholes-Merton-prijsberekening voor call- en putopties |
Bekijk screenshot van dit werkblad |
Gebruiksinstructie
Introductie
De oorspronkelijke Black-Scholes-vergelijking, die de prijs C van een Europese calloptie berekent, ziet er als volgt uit:
C = S * N(d1) - E * e-r*t * N(d2)
Met opneming van de parameter q luidt de Black-Scholes-Merton-variant:
C = S * e-q*t * N(d1) - E * e-r*t * N(d2)
De oorspronkelijke Black-Scholes-vergelijking die de prijs P van een Europese putoptie berekent, luidt:
P = -S * N(-d1) - E * e-r*t * N(-d2)
Met opneming van de parameter q luidt de Black-Scholes-Merton-variant:
P = -S * e-q*t * N(-d1) + E * e-r*t * N(-d2)
De hulpvariabele d1 kent in het oorspronkelijke model de volgende opbouw:
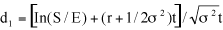
Merton heeft d1 als volgt uitgebreid:
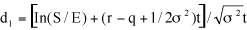
De hulpvariabele d2 blijft, als afgeleide van d1 ongewijzigd:
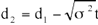
Personeelsmanagement

Heeft u ook een verantwoordelijkheid in personeelsmanagement? Kijk dan ook op HR Praktijk voor zekerheid over wetten en regels!
Gerelateerde Excelsheets
-
 Covariantie, correlatie en regressie bij diversificatie
Covariantie, correlatie en regressie bij diversificatie
-
 Een optie op de oliemarkt als casus
Een optie op de oliemarkt als casus
-
 Een rendementsrisicomatrix in Excel
Een rendementsrisicomatrix in Excel
-
 Een vastrentende lening door een swap variabel maken
Een vastrentende lening door een swap variabel maken
-
 Forward bij een verwachte rentedaling
Forward bij een verwachte rentedaling
-
 Forward bij een verwachte rentestijging
Forward bij een verwachte rentestijging
-
 Futures
Futures
-
 Gevoeligheidratio's bij de prijsvorming van opties
Gevoeligheidratio's bij de prijsvorming van opties
-
 Het Black-Scholes-Merton-model
Het Black-Scholes-Merton-model
-
 Het Black-Scholes-model
Het Black-Scholes-model
-
 Historische en impliciete volatiliteit
Historische en impliciete volatiliteit
-
 Koop call-opties
Koop call-opties
-
 Koop putopties
Koop putopties
-
 On-balance hedging tegen renterisico's
On-balance hedging tegen renterisico's
-
 Optieprijzen berekenen met het binomiale model
Optieprijzen berekenen met het binomiale model
-
 Opties Algemeen
Opties Algemeen
-
 Opties op (staats)obligaties. beschermende werking...
Opties op (staats)obligaties. beschermende werking...
-
 Opties op (staats)obligaties: callopties in...
Opties op (staats)obligaties: callopties in...
-
 Overige afschermende rente-instrumenten: caps,...
Overige afschermende rente-instrumenten: caps,...
-
 Rendement en risico van investeringen en beleggingen
Rendement en risico van investeringen en beleggingen
-
 Renterisico's meten: yieldcurve en duration
Renterisico's meten: yieldcurve en duration
-
 Risicometing bij verschillende beleggingsvormen:...
Risicometing bij verschillende beleggingsvormen:...
-
 Valutaswaps
Valutaswaps
-
 Valutatermijntransacties
Valutatermijntransacties
-
 Van een variabel rentende belegging door een swap...
Van een variabel rentende belegging door een swap...

