Afschrijvingsfuncties
Er zijn verschillende methodes om de afschrijvingen van uw activa te berekenen. De meest bekende zijn:
- een vast percentage van de (historische) aanschafprijs ofwel lineaire afschrijving in een aantal jaar;
- een vast percentage van de boekwaarde (een vorm van degressief afschrijven);
- de sum of the years digits-methode (eveneens een vorm van degressief afschrijven).
Excel beschikt over vijf functies voor het berekenen van de afschrijvingen van uw activa volgens verschillende methodes. Hier
bespreken we aan de hand van verschillende voorbeelden de functies LIN.AFSCHR, DB, SYD, DDB en VDB.
De functie LIN.AFSCHR – lineaire afschrijving
Deze functie berekent de lineaire afschrijving van activa per periode. Lineair houdt in dat de afschrijving gelijk blijft
gedurende de hele levensduur van de activa. De functie ziet er als volgt uit:
=LIN.AFSCHR(kosten, restwaarde, duur).
De (verplichte) argumenten bij deze functie zijn:
- kosten: de historische aanschafkosten van de activa;
- restwaarde: de verwachte resterende waarde van de activa aan het eind van de economische levensduur;
- duur: het aantal termijnen waarover de activa wordt afgeschreven. Dit kan in jaren worden opgegeven, maar ook in kwartalen, maanden,
enzovoort. De berekende afschrijving is dan natuurlijk eveneens per jaar respectievelijk kwartaal of maand.
Voorbeeld 1
Een machine van € 120.000 heeft een restwaarde van € 5.000 en een levensduur van tien jaar. Om de afschrijving per jaar te
berekenen is (in het Excel-bestand Afschrijvingsfuncties.xls) de volgende tabel opgezet:
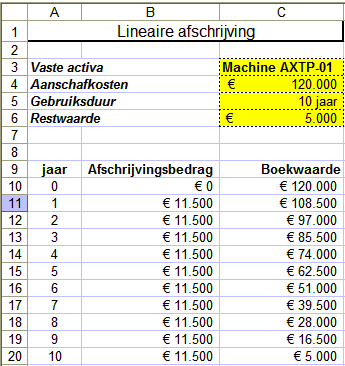
In de cellen B11 tot en met B20 wordt het termijnbedrag voor de afschrijving als volgt berekend:
=LIN.AFSCHR($C$4;$C$6;$C$5)
De functie DB – declining balance
Deze functie gaat uit van een 'fixed declining balance', oftewel van vaste degressieve afschrijving. Hij berekent de afschrijving
van activa voor één bepaalde periode waarbij afgeschreven wordt met een vast percentage van de boekwaarde (kosten van de activa
minus de som van reeds afgeschreven bedragen in voorgaande jaren). De functie ziet er als volgt uit:
=DB(kosten; restwaarde; duur; termijn; maand).
De verplichte argumenten bij deze functie zijn:
- kosten: de historische aanschafkosten van de activa;
- restwaarde: de verwachte resterende waarde van de activa aan het eind van de economische levensduur;
- duur: het aantal termijnen waarover de activa wordt afgeschreven;
- termijn: de termijn waarvoor de afschrijving berekend moet worden (bijvoorbeeld het derde jaar ofwel termijn 3).
Deze functie heeft daarnaast het volgende optionele argument:
- maand: het aantal maanden dat in het eerste jaar afgeschreven moet worden. Laat u dit argument leeg, dan gaat Excel ervan uit dat
in het eerste jaar twaalf maanden afgeschreven worden.
Let op: De argumenten duur en termijn moeten in dezelfde tijdseenheid weergegeven worden (bijvoorbeeld beide in jaren of in maanden).
Voorbeeld 2
In het volgende voorbeeld wordt de functie DB gebruikt voor het berekenen van de afschrijving van een machine met een boekwaarde
van € 150.000, een geschatte restwaarde van € 2.000 en een levensduur van 10 jaar.
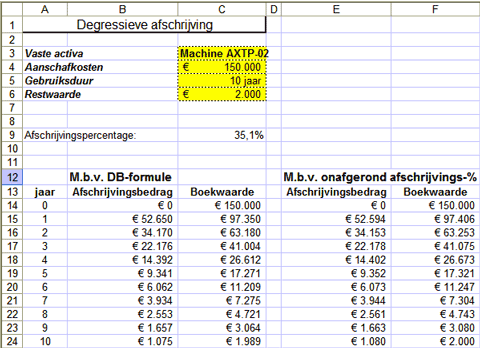
In cel B15 vindt u de volgende formule:
=DB($C$4;$C$6;$C$5;A15)
Het te hanteren jaarlijkse afschrijvingspercentage wordt berekend met behulp van de volgende formule:
1 – [(restwaarde/kosten)(1/duur)]
Het feit dat de boekwaarde aan het eind van de afschrijvingsperiode bij gebruik van de functie DB niet exact op de geplande
restwaarde uitkomt (€ 1.989 in plaats van € 2.000), wordt veroorzaakt doordat Excel het te hanteren afschrijvingspercentage
eerst afrondt op drie cijfers achter de komma (0,351 ofwel 35,1% in het bovenstaande voorbeeld), en daarmee vervolgens de
afschrijvingen per periode bepaalt.
De functie SYD – Sum of the Years Digits
De Sum of the Years Digits-methode is een vorm van afschrijven waarbij de resterende levensduur van de activa als wegingsfactor
wordt gehanteerd en waarbij naar rato van de nog resterende levensduur wordt afgeschreven: hoe langer de nog resterende levensduur,
hoe hoger de afschrijvingen in het betreffende jaar. Dit resulteert aldus in degressieve afschrijvingen. De functie ziet er
als volgt uit:
=SYD(kosten; restwaarde; duur; termijn).
De (verplichte) argumenten bij deze functie zijn:
- kosten: de historische aanschafkosten van de activa;
- restwaarde: de verwachte resterende waarde van de activa aan het eind van de economische levensduur;
- duur: het aantal termijnen waarover de activa wordt afgeschreven;
- termijn: de termijn waarvoor de afschrijving moet worden berekend.
Let erop dat ook nu de argumenten duur en termijn in dezelfde tijdseenheid moeten worden weergegeven (bijvoorbeeld beide in jaren of maanden).
Voorbeeld 3
Een machine kost € 150.000, heeft een levensduur van 9 jaar en een geschatte restwaarde van € 9.000. De berekening voor de
afschrijving per jaar ziet er als volgt uit:
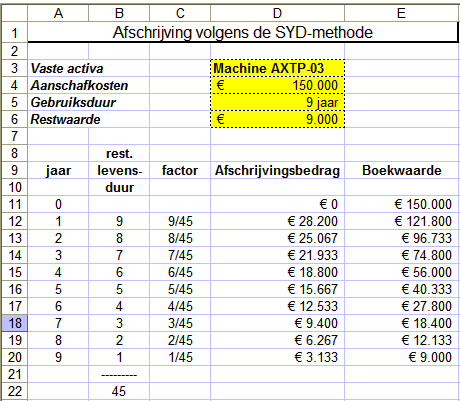
In cel D12 vindt u de volgende formule:
=SYD($D$4;$D$6;$D$5;A12)
Excel kent nog twee andere functies die gebruikt kunnen worden voor het berekenen van afschrijvingen van activa. Deze functies
zullen echter nauwelijks gebruikt worden, omdat de betreffende afschrijvingsmethoden in de praktijk (bijna) nooit worden toegepast.
Voor de volledigheid worden ze hier toch besproken.
De functie DDB – double declining balance
Deze functie (ook wel dubbele degressieve afschrijvingsmethode genoemd) berekent de versnelde afschrijving van activa, waarbij
de gebruiker de snelheid kan opgeven. Bij deze methode wordt (evenals bij de functie DB) de afschrijving berekend als een
percentage van de boekwaarde van de activa. Het te hanteren afschrijvingspercentage wordt echter op een andere wijze bepaald.
De functie ziet er als volgt uit:
=DDB(kosten; restwaarde; duur; termijn; factor).
De argumenten kosten, restwaarde, duur en termijn hebben dezelfde betekenis als bij de hiervoor besproken functies. Het optionele argument factor kunt u gebruiken om de snelheid waarmee afgeschreven moet worden aan te geven. Laat u dit argument leeg, dan zal Excel de
standaardwaarde 2 (dubbele degressieve afschrijving) gebruiken.
Het te hanteren afschrijvingspercentage wordt bepaald met behulp van de volgende formule:
(factor/duur) ofwel (factor x 1/duur)
Dit betekent dat het afschrijvingspercentage in eerste instantie wordt bepaald alsof het gaat om lineaire afschrijving (namelijk
1/duur) en vervolgens wordt vermenigvuldigd met een (optioneel door de gebruiker aan te geven) factor om een versnelde afschrijving
te krijgen. Er wordt echter niet afgeschreven van de aanschafwaarde (zoals bij lineaire afschrijving) maar van de boekwaarde.
Afhankelijk van de investeringsbedragen en afschrijvingstermijnen kan dit erin resulteren dat de activa niet volledig binnen
de aangegeven gebruiksduur worden afgeschreven, of dat de activa al voor het einde van de gebruiksduur volledig zijn afgeschreven.
De volgende voorbeelden zullen dit duidelijk maken.
Voorbeeld 4a
In het volgende voorbeeld wordt de functie DDB gebruikt om het af te schrijven bedrag per jaar te berekenen voor een investering
van € 240.000, met een restwaarde van € 30.000 en een levensduur van 10 jaar:
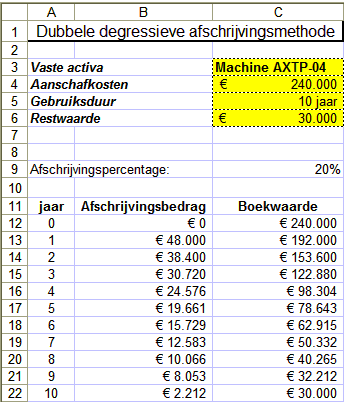
In cel B13 is de volgende formule gebruikt:
=DDB($C$4;$C$6;$C$5;A13;2)
De afschrijving komt in dit voorbeeld netjes uit op de geplande restwaarde na het laatste jaar van de gebruiksduur.
Voorbeeld 4b
In de volgende voorbeelden wordt dezelfde functie gebruikt. Ditmaal gaat het om een investering van € 200.000, met een levensduur
van 10 jaar en een restwaarde van € 50.000, respectievelijk € 10.000:
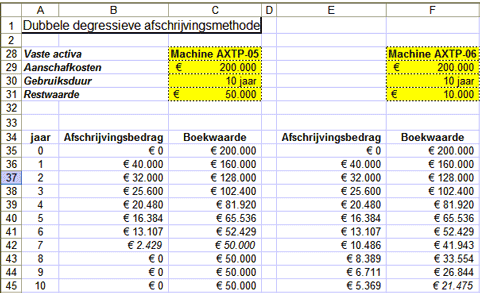
Ditmaal is de investering in het linkervoorbeeld al na het zevende jaar afgeschreven tot de verwachte restwaarde, en wordt
er in de jaren acht tot en met tien niet meer afgeschreven. In het rechtervoorbeeld is de investering na tien jaar (de verwachte
levensduur) juist nog niet volledig afgeschreven tot de verwachte restwaarde.
De functie VDB – variable declining balance
Indien u het afschrijvingsbedrag wilt weten van activa over een periode of een aantal periodes van de levensduur van de activa,
dan kunt u gebruikmaken van de functie VDB. Deze functie (variabele degressieve afschrijving) berekent de afschrijving van
activa over een periode (of een aantal periodes) met behulp van de dubbele degressieve afschrijvingsmethode. De functie ziet
er als volgt uit:
=VDB(kosten; restwaarde; duur; begin_periode; eind_periode;
factor; geen_omschakeling).
De verplichte argumenten van deze functie zijn:
- kosten, restwaarde en duur hebben dezelfde betekenis als bij de hiervoor besproken functies;
- begin_periode is de eerste termijn waarover u de afschrijving wilt berekenen. Let op: als begin_periode = 4 zal Excel de eerste vier periodes overslaan, en dus bij periode 5 beginnen!
- eind_periode is de laatste termijn waarover u de afschrijving wilt berekenen.
De argumenten duur, begin_periode en eind_periode moeten in dezelfde eenheid weergegeven worden (bijvoorbeeld jaar, kwartaal of maand).
De optionele argumenten bij deze functie zijn:
- factor: dit argument kunt u gebruiken om de snelheid aan te geven waarmee moet worden afgeschreven. Laat u dit argument leeg, dan
zal Excel de standaardwaarde 2 (dubbele degressieve afschrijving) gebruiken;
- geen_omschakeling: dit argument kunt u gebruiken als u wilt dat Excel overschakelt naar lineaire afschrijving als de lineaire afschrijving groter
is dan de afschrijving op basis van de degressieve afschrijvingsmethode. Geeft u als waarde ONWAAR of laat u het argument
weg, dan zal Excel overschakelen naar lineair; is de waarde van geen_omschakeling WAAR, dan zal Excel niet overschakelen naar lineair.
Voorbeeld 5a
Voor een machine met een boekwaarde van € 300.000, een restwaarde van € 25.000 en een levensduur van 10 jaar wilt u weten
hoeveel u in de eerste twee kwartalen van jaar 2 tezamen (kwartaal 5 plus kwartaal 6) moet afschrijven:
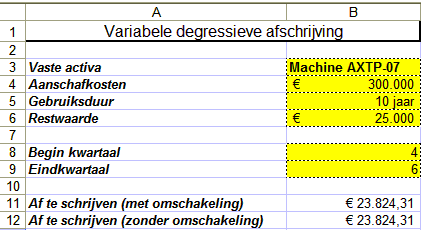
In cel B11 vindt u de volgende formule:
=VDB($B$4;$B$6;$B$5*4;B8;B9;2;ONWAAR)
In cel B12 vindt u de volgende formule:
=VDB($B$4;$B$6;$B$5*4;B8;B9;2;WAAR)
Zoals u ziet, gebruiken we bij het argument duur de berekening 'gebruiksduur*4' om van jaar naar kwartaal om te schakelen. In cel B11 geven we ook aan dat Excel mag overschakelen naar een lineaire afschrijving als de afschrijving volgens deze methode groter
is dan volgens de dubbele degressieve afschrijvingsmethode (argument geen_omschakeling = ONWAAR). Dit resulteert echter (nog) niet in een ander afschrijvingsbedrag dan in B12. Blijkbaar is de afschrijving op basis van dubbele degressieve afschrijving nog steeds groter dan op basis van lineaire afschrijving.
Voorbeeld 5b
U wilt voor dezelfde machine weten hoeveel u in de eerste twee kwartalen van jaar 8 tezamen (kwartaal 29 plus kwartaal 30)
moet afschrijven:
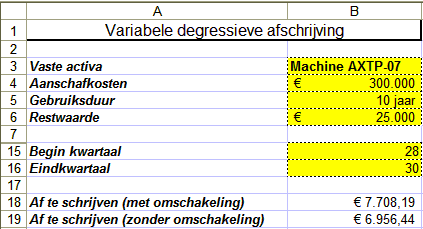
In cel B18 vindt u de volgende formule:
=VDB($B$4;$B$6;$B$5*4;B15;B16;2;ONWAAR)
In cel B19 vindt u de volgende formule:
=VDB($B$4;$B$6;$B$5*4;B15;B16;2;WAAR)
Blijkbaar is voor de betreffende perioden de lineaire afschrijving (B18) groter dan de afschrijving volgens de dubbele degressieve afschrijvingsmethode (B19).
Vergelijking afschrijvingsfuncties
Ter afsluiting van deze paragraaf maken we een vergelijking van de verschillende afschrijvingsmethoden.
Voorbeeld 6
Een machine met een boekwaarde van € 150.000, een geschatte restwaarde van € 10.000 en een levensduur van 10 jaar kan volgens
de vier verschillende afschrijvingsmethodes als volgt worden afgeschreven:
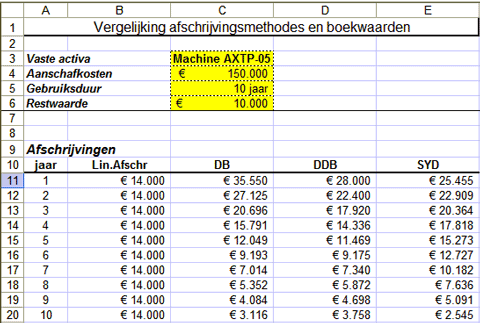
De bijbehorende boekwaarden vindt u in de onderstaande tabel:
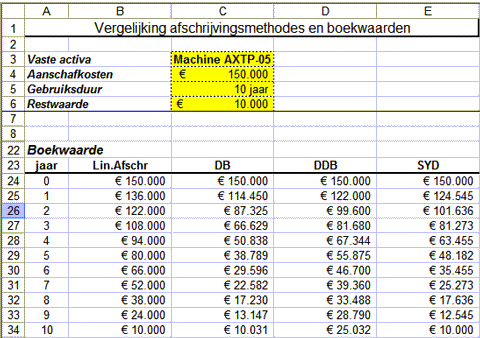
Zoals u in bovenstaande tabellen kunt zien, zijn de bedragen die in een bepaald boekjaar ten laste van het resultaat kunnen
worden gebracht, nogal verschillend, afhankelijk van de gebruikte afschrijvingsmethode.
Vakinformatie 
Calculatie afschrijvingen op investeringen in...