Rendementsberekeningen bij aandelen: te verwachten rendement
Verwachte rendementen op aandelen zijn eenvoudig te berekenen met behulp van de functie IR.SCHEMA. Excel is in staat het rendement te bepalen aan de hand van een in de toekomst gelegen datumschema in combinatie met een of meerdere cashflows. De berekening werkt op basis van samengestelde rente en 365 renterekendagen per jaar.
Werkbladen in deze Excelsheet
|
Werkblad Rendementsberekeningen bij aandelen: verwacht rendement |
Bekijk screenshot van dit werkblad |
Gebruiksinstructie
Introductie
Onder effecten verstaan we verhandelbare waardepapieren zoals aandelen, obligaties, schatkistpapier, pandbrieven en opties.
Het beleggen in effecten kan worden beschouwd als een normale investeringsbeslissing waarbij de belegger ernaar streeft om gegeven een aanvaardbare risicograad – een zo hoog mogelijk rendement te behalen.
In dit verband kan worden verwezen naar de netto contante waarde en de interne rentabiliteit van investeringsprojecten.
Ofschoon het in de praktijk niet altijd eenvoudig is om tot een eenduidige methode van rendementsberekening voor effecten te komen, blijkt de volgende algemene vergelijking in veel gevallen toepasbaar:
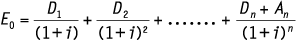
of in termen van interne rentabiliteit:
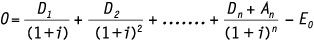
waarbij:
| E0 | = | de uitgiftekoers of aankoopprijs op tijdstip 0 |
| D1 t/m Dn | = | periodieke uitkeringen over de perioden 1 t/m n |
| An | = | de (verwachte) verkoop- of aflossingsprijs aan het eind van periode n |
| i | = | de te behalen of de gewenste rendementsvoet |
De algemene vergelijking kan in twee richtingen worden uitgezet:
- Vanuit het verleden naar het heden
In dit geval zijn alle parameters ten behoeve van de berekening van het rendement i bekend en spreken we van een gerealiseerd of behaald rendement. - Vanuit het heden naar de toekomst
In dit tweede geval staan we voor de beslissing om te beleggen in effecten, gegeven de aankoopprijs (E) en de verwachtingen ten aanzien van de overige parameters (D1tot en met Dn en An).
Op basis hiervan kunnen we het te verwachten rendement bepalen.
In aansluiting op de algemene vergelijking kunnen we bij de berekening van het rendement op effecten gebruikmaken van de functie IR.SCHEMA(waarden;data;schatting).
Deze vergelijking heeft onder Excel de volgende gedaante:
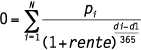
met:
| di | = | i-e betaaldatum |
| d1 | = | 0-e betaaldatum |
| pi | = | i-e betaling |
| rente | = | rendement |
In deze vergelijking wordt standaard uitgegaan van 365 rentedagen per jaar.
Dit kan enigszins afwijken van specifiek op waardepapieren gerichte Excel-functies waarbij gebruikgemaakt kan worden van een afwijkend datumschema (in de vorm van het argument soort-jaar).
Deze functies, die specifiek op vastrentende waardepapieren betrekking hebben, behandelen we ook nog uitgebreid.
Een aandeel is een eigendomsbewijs in een besloten of naamloze vennootschap. Een aandeelhouder ontvangt als vergoeding geen rente maar dividend. Beleggen in aandelen is risicovol en dividenduitkeringen en koersontwikkelingen zijn daarbij onzekere elementen voor de aandeelhouder.
De aantrekkelijke keerzijde hiervan is dat met aandelen gemiddeld hogere rendementen zijn te behalen dan met andere minder risicovolle beleggingsvormen, zoals obligaties.
De prijsvorming van aandelen is afhankelijk van meerdere factoren. Volgens algemeen aanvaarde theorieën is de koers van een aandeel gelijk aan de contante waarde van de verwachte dividenduitkeringen en de waarde bij verkoop.
Personeelsmanagement

Heeft u ook een verantwoordelijkheid in personeelsmanagement? Kijk dan ook op HR Praktijk voor zekerheid over wetten en regels!
Gerelateerde Excelsheets
-
 Berekening achterliggende grootheden bij IR.SCHEMA
Berekening achterliggende grootheden bij IR.SCHEMA
-
 Berekening functies PRIJS.NOM en RENDEMENT aan de...
Berekening functies PRIJS.NOM en RENDEMENT aan de...
-
 Berekening hoogte van de couponrente met functies...
Berekening hoogte van de couponrente met functies...
-
 Berekening prijs en rendement bij afwijkende eerste...
Berekening prijs en rendement bij afwijkende eerste...
-
 Berekening prijs en rendement bij afwijkende laatste...
Berekening prijs en rendement bij afwijkende laatste...
-
 Berekening prijs en rendement bij rentebetaling op...
Berekening prijs en rendement bij rentebetaling op...
-
 Berekeningen met schatkistpapierfuncties
Berekeningen met schatkistpapierfuncties
-
 Couponberekeningen met COUP-functies
Couponberekeningen met COUP-functies
-
 Disconteringsberekening met functies DISCONTO en...
Disconteringsberekening met functies DISCONTO en...
-
 Disconteringsberekening met functies Opbrengst en...
Disconteringsberekening met functies Opbrengst en...
-
 Duration-berekening handmatig
Duration-berekening handmatig
-
 Duration-berekening met functies AANG.DUUR en DUUR
Duration-berekening met functies AANG.DUUR en DUUR
-
 Duration-berekening 'Zero-bond' (geen tussentijdse...
Duration-berekening 'Zero-bond' (geen tussentijdse...
-
 Herleiding uitkomst functie RENDEMENT met de functie...
Herleiding uitkomst functie RENDEMENT met de functie...
-
 Rendementsberekeningen bij aandelen: behaald rendement
Rendementsberekeningen bij aandelen: behaald rendement
-
 Rendementsberekeningen bij aandelen: te verwachten...
Rendementsberekeningen bij aandelen: te verwachten...
-
 Rendementsberekeningen bij obligatieleningen:...
Rendementsberekeningen bij obligatieleningen:...
-
 Rendementsberekeningen bij obligatieleningen: te...
Rendementsberekeningen bij obligatieleningen: te...

