Prijsvorming op de geldmarkt
Prijzen voor vermogenstitels op de geldmarkt worden bepaald door de te verwachten cashflows – gedetailleerd in rekendagen – te berekenen en te verdisconteren.
Werkbladen in deze Excelsheet
|
Werkblad Prijsvorming kortlopende obligaties |
Bekijk screenshot van dit werkblad |
Gebruiksinstructie
Introductie
Geldmarktberekeningen luisteren uiterst nauw en zijn gebaseerd op (rente)dagen en onderliggende dataschema's.
Dit volgens het principe:
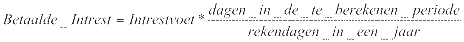
Ten aanzien van het aantal rekendagen in een jaar (zie noemer) wordt onderscheid gemaakt tussen de volgende rekenstelsels:
- standaard 365 dagen, ook in geval van een schrikkeljaar met 366 dagen;
- standaard 360 dagen;
- het werkelijk aantal dagen (365 of 366).
Relatief vaak voorkomende rekenconventies zijn 'ACT/365' en 'ACT/360', wat wil zeggen dat in de teller gerekend wordt met het werkelijk ('ACT') aantal dagen en in de noemer standaard met 365 respectievelijk 360 dagen.
Omrekening van het ene naar het andere stelsel vindt daarbij als volgt plaats:
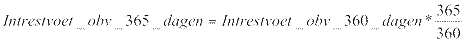
respectievelijk
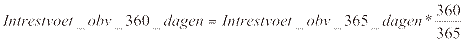
Binnen de specifieke geldmarktfuncties van Excel wordt gewerkt met de vijf mogelijke combinaties:
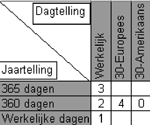
Daarnaast wijzen we op de functie DAGEN360(begindatum;einddatum;methode) die het aantal dagen tussen twee datums op basis van een jaar met 360 dagen (twaalf maanden met dertig dagen) berekent.
Personeelsmanagement

Heeft u ook een verantwoordelijkheid in personeelsmanagement? Kijk dan ook op HR Praktijk voor zekerheid over wetten en regels!
Gerelateerde Excelsheets
-
 Beheer goederenvoorraden, voorraadverschillen en...
Beheer goederenvoorraden, voorraadverschillen en...
-
 Beheer werkkapitaal: crediteurentermijn
Beheer werkkapitaal: crediteurentermijn
-
 Beheer werkkapitaal: debiteurentermijn
Beheer werkkapitaal: debiteurentermijn
-
 Bepalen van de gemiddelde voorraadtermijn
Bepalen van de gemiddelde voorraadtermijn
-
 Berekening rente en aflossingsschema voor een lening
Berekening rente en aflossingsschema voor een lening
-
 Financieringskasstroom
Financieringskasstroom
-
 Inkomsten naar productgroepen en verdeling in de tijd
Inkomsten naar productgroepen en verdeling in de tijd
-
 Inkomstenkant – debiteurentermijn
Inkomstenkant – debiteurentermijn
-
 Inkomstenkant – geplande kortingen
Inkomstenkant – geplande kortingen
-
 Inkomstenkant – omzetplanning
Inkomstenkant – omzetplanning
-
 Investeringskasstroom
Investeringskasstroom
-
 Liquiditeitsprognose totaaloverzicht
Liquiditeitsprognose totaaloverzicht
-
 Liquiditeitsprognose vergelijking werkelijkheid en...
Liquiditeitsprognose vergelijking werkelijkheid en...
-
 Maandelijkse btw-afdrachten
Maandelijkse btw-afdrachten
-
 Matrix doorlooptijd en matrix crediteurentermijn
Matrix doorlooptijd en matrix crediteurentermijn
-
 Overige operationele kasstroom
Overige operationele kasstroom
-
 Prijsvorming op de geldmarkt
Prijsvorming op de geldmarkt
-
 Relatie marktprijs, marktrente en aantal rentedagen
Relatie marktprijs, marktrente en aantal rentedagen
-
 Rendementen berekenen met het geldmarktmodel
Rendementen berekenen met het geldmarktmodel
-
 Samenvatting van uitgaven
Samenvatting van uitgaven
-
 Uitgaven naar productgroepen en verdeling in de tijd
Uitgaven naar productgroepen en verdeling in de tijd
-
 Uitgavenkant – omzetplanning
Uitgavenkant – omzetplanning

