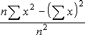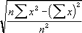Berekenen risicograad bij overname

Een hogere rendementsverwachting – bij het vormen van een beleggingsportefeuille of het maken van investeringsselecties – doorgaans gepaard gaat met een hogere risicograad.

Het Capital Asset Pricing Model (CAPM) is een rekenmodel dat expliciet een link legt tussen risico en rendement.

Het CAPM gaat ervan uit dat er – onder transparante marktomstandigheden – een verband bestaat tussen het te verwachten rendement en het te lopen risico, waarbij hogere rendementen alleen te behalen zijn ten koste van een groter risico.

Beleggers en vermogensverschaffers verlangen als beloning een risicovrij rendement plus een risico-opslag waarin het marktrisico besloten ligt.

Dit deel van het marktrisico, dat ook wel aangeduid wordt als het 'systematisch' risico, kan volgens de CAPM-theorie niet door diversificatie van een investerings- of beleggingsportefeuille worden geëlimineerd.

Het systematische risico wordt binnen het CAPM uitgedrukt met de bèta of het symbool ß.

Met de bèta wordt de gevoeligheid van het rendement van een investering of belegging weergegeven ten opzichte van het rendement van de betreffende markt (of de index) als geheel.

Een bètawaarde van nul betekent dat de belegging risicovrij is, bij een waarde van 1 is de belegging even risicovol (volatiel) als de markt, bij een waarde van 2 is de belegging tweemaal zo risicovol als de markt.

De formules

De rendementseis van vermogensverschaffers E(R_i) wordt binnen het CAPM berekend door het risicovrije rendement R_f op te tellen bij het product van de bèta (ß) en de marktpremie. Die marktpremie is gelijk aan het verschil tussen het marktrendement E(R_m) en het risicovrije rendement R_f:

E(R_i)= R_f + ß_im(E(R_m) - R_f

met

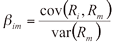
In de noemer staat de covariantie opgenomen tussen de rendementsontwikkeling R_m van een efficiënte marktportefeuille (lees: het marktrendement of de index) en een individueel aandeel R_i.

In de teller staat de variantie opgenomen van de rendementsontwikkeling van een efficiënte marktportefeuille.

De begrippen variantie, standaarddeviatie en covariantie bespraken we eerder in deel 970 bij de spreiding van investeringen en beleggingen, hieronder enige 'opfrissing'.

• De variantie (Var) – als spreidingsmaatstaf rond het rekenkundig gemiddelde voor een steekproef met n waarnemingen (ook wel aangeduid als σ²_x) – berekenen we als:

  

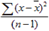
  waarbij x de verschillende individuele rendementen weergeeft en x het rekenkundig gemiddelde over alle rendementen. De parameter n geeft het aantal waarnemingen in de steekproef weer.

• De standaarddeviatie (ook wel aangeduid als σ_x ), is de wortel van de variantie:

  

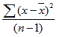
• Waar de variantie en de standaarddeviatie maatstaven vormen voor de mate van spreiding van de waarnemingen binnen één populatie van waarnemingen, meet de covariantie de samenhang van de afwijkingen in twee waarnemingspopulaties X en Y door middel van de volgende vergelijking:

  

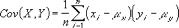
  waarbij x_i staat voor de verschillende individuele waarnemingen in de populatie X, en Y_i in de populatie Y. De variabelen U_x en U_y staan voor het rekenkundig gemiddelde van de populaties X en Y. De parameter n ten slotte geeft de omvang van het aantal waarnemingen in de populaties X en Y weer.

Uitgaand van het werkblad Basisrekenmodel bedrijfswaardering overweegt het management van onderneming Y overname van de niet beursgenoteerde onderneming Z. Het over te nemen bedrijf Z is qua activiteiten, opbouw en marktprofiel goed vergelijkbaar met de wel beursgenoteerde onderneming X.

Bij de vaststelling van de rendementseis (lees: disconteringsvoet) bij overname laat het management van onderneming Y zich leiden door de maandelijkse rendementsontwikkeling van de marktindex in combinatie met de rendementsontwikkeling van het beursgenoteerde vergelijkbare aandeel X. Dit over een periode van de laatste 5 jaar.

Werkblad Maandelijkse rendementsontwikkeling

In kolom B staat de beursindex aangegeven over de periode van 1 december 2002 (A65) tot 1 december 2007 (A5). Uit praktische overwegingen hebben we alleen de periode van 1 december 2005 tot 1 december 2007 afgedrukt.

In kolom C is over dezelfde periode de koers van onderneming X aangegeven.

Werkblad Bepalen van de bèta bij overname

In dit werkblad, dat is gekoppeld aan het werkblad Maandelijkse rendementsontwikkeling, hebben we in B13:B73 respectievelijk C13:C73 de maandelijkse index- en de koersontwikkeling van onderneming X opgenomen (ook hiervan hebben we om praktische reden alleen het bovenste deel afgedrukt).

In het bereik D13:D73 en E13:E73 hebben we vervolgens het verschil bepaald tussen de risicovrije voet op maandbasis (E3=0,4167%) en de overeenkomstige cellen in de het bereik B13:B72 en C13:C72:

Werkblad Maandelijkse rendementsontwikkeling

Het gemiddelde van de beursindex en de koers is berekend in B1 en C1:

B1=GEMIDDELDE(B5:B65);
C1=GEMIDDELDE(C57:C65).

De standaarddeviatie is berekend in B2 en C2:

B2=STDEVP(B5:B65);
C2=STDEVP(C5:C65).

Werkblad Bepalen van de bèta bij overname

Met deze gegevens kunnen we het systematische risico (de bèta) bepalen van onderneming X en vervolgens het CAPM vullen.

De teller cov(R_i,R_m) van de bèta hebben we in E4 berekend met behulp van de covariantiefunctie:

=COVARIANTIE(D13:D73;E13:E73)

De noemer var(R_m)van de bèta hebben we in E5 berekend met behulp van de variantiefunctie:

=VARP(D13:D73)

De ß_im zijnde het quotiënt (=E4/E5) bedraagt 0,8715 in cel E6.

Hiermee hebben we alle ingrediënten om de vergelijking voor de vereiste rendementsvoet (lees: de disconteringsvoet voor de overname van onderneming Y) te completeren:

E(R_i) = R_f + ß_im(E(R_m) - R_f) = 0,4167 + 0,8715(E(R_m) - 0,4167) = 0,8715*E(R_m) + 0,011

Werkblad Samenstellen regressielijn

Met behulp van de gegevens uit het werkblad Bepalen van de bèta bij overname hebben we in het werkblad Samenstellen een regressielijn samengesteld.

De hellingshoek van de regressielijn (0,8715) kan – alternatief – ook berekend worden met behulp van de functie RICHTING.

In cel E7 hebben we deze functie als volgt opgenomen:

=RICHTING('sheet 3'!E13:E73;'sheet 3'!D13:D73)

Het snijpunt met de y-as berekenen we met behulp van de gelijknamige functie SNIJPUNT() in cel E8:

=SNIJPUNT(sheet3!E13:E73;sheet3!D13:D73)

De mate van correlatie van het spreidingsdiagram met de regressielijn blijkt uit de correlatiecoëfficiënt R. Het kwadraat daarvan – ook wel aangeduid als de determinatiecoëfficiënt R² – is onder E9 berekend met behulp van de functie CORRELATIE:

=(CORRELATIE(sheet3!D13:D73;sheet3!E13:E73))^2

De regressielijn die we hebben weergegeven is in de financiële literatuur ook bekend als de vermogensmarktlijn of de Security Market Line (SML).

Een hoge bèta betekent een hoog marktrisico, waarvoor de vermogensverschaffer extra rendement wenst.

De gevonden bèta van 0,8715 is in dit verband relatief laag te noemen en ligt onder het niveau van die van de marktportefeuille met een bèta van precies 1.

(Als je de proef op de som wil nemen kun je voor een bèta van 1 de koersgegevens in het bereik C5:C65 gelijk maken aan die van het bereik B5:B65, de marktindexontwikkeling!)

NB:
Bij de berekening van de standaarddeviatie (sheet 2: B2 en C2) en de variantie (sheet 3: E5) zijn we uitgegaan van de Excel-functies STDEVP respectievelijk VARP.

De uitkomst van deze functies wijkt enigszins af van die van de soortgelijke functies STDEV en VAR omdat ze uitgaan van een gehele populatie. De functies STDEV en VAR gaan uit van een steekproef en maken vervolgens een schatting van de standaarddeviatie en de variantie op basis van de steekproef. We veronderstellen in het voorbeeld 'een volledige populatie van koerswaarnemingen (60) per de eerste van de maand over een vastgestelde periode van vijf jaar'. De onderliggende vergelijkingen voor de variantie en de standaarddeviatie zien er, bij een populatieomvang van n, als volgt uit:

respectievelijk

Rijen of kolommen om en om arceren in een reeks

In het werkblad Bepalen van de bèta bij overname hebben we vanaf rij 13 de rijen om en om lichtgroen gearceerd.

Het om en om arceren van rijen (of kolommen) kunt u instellen met behulp van voorwaardelijke opmaak.

Dit hebben we als volgt gedaan na de menuoptie Opmaak – Voorwaardelijke opmaak en het vooraf selecteren van het te arceren bereik:

Onder het vakje Voorwaarde 1 is gekozen voor de optie Formule is, waarna we als voorwaardelijke formule hebben opgenomen dat de lichtgroene opmaak (te kiezen via de knop Opmaak) van toepassing is op alle even rijen. Dit zijn de rijen die na deling door 2 een integer ofwel geheel getal opleveren:

=RIJ($A13)/2=INTEGER(RIJ($A13)/2).

In het op te maken bereik wordt in de formule altijd verwezen naar de cel linksboven, in dit geval dus A13.