Introductie
Globaal zijn er twee soorten financiële schema's te onderscheiden: cashflow- en amortisatieschema's.
Bij cashflowschema's is sprake van een continue in- en uitstroom aan cashflows, zonder dat sprake is van een duidelijk gemarkeerd
eindpunt.
Dit is bij amortisatieschema's, waarbij het doel is om een schuld te delgen of een lening af te lossen, wel het geval: een
amortisatieschema kent (doorgaans) een eindsaldo van 0.
Amortisatieschema's en financiële functies
Onder Berekening jaarlijkse annuïteit bestudeerden we hoe een eenvoudig amortisatieschema voor een annuïtaire aflossing in elkaar steekt en hoe de bijbehorende
betalingen kunnen worden berekend met behulp van de functie BET. Daarnaast zijn in Excel specifieke functies beschikbaar om
de intrest- en de aflossingscomponent te berekenen voor annuïtaire leningen. Op jaarbasis zijn dit de functies IBET en PBET,
op cumulatieve basis de functies CUM.RENTE en CUM.HOOFDSOM. Deze functies bekeken we onder Berekening annuïteit op meerjarige basis.
Doel van deze tool
Na het downloaden van het model van de Microsoft-site (http://office.microsoft.com/en-us/excel/HA010346401033.aspx) hebben we het volgende voorbeeld ingebracht:
- een annuïtaire lening van € 100.000 (D6);
- een jaarlijkse intrestvoet van 7 % (D7);
- vier jaarlijkse kwartaaltermijnen (D9);
- ingangsdatum 1-1-2008 (D10);
- geen extra betaling (optioneel) (D11 en kolom E onder 'Extra Payment').
Resultaten
Resultaat_1
In H6 wordt vervolgens met behulp van de functie BET de annuïteit per kwartaal berekend:
| H6 |
=ALS(Values_Entered;-BET(Interest_Rate/Num_Pmt_Per_Year;Loan_
Years*Num_Pmt_Per_Year;Loan_Amount);"") = € 9.311,38
|
In het eerste deel van de formule zien we het argument =ALS(Values_Entered;.
Het benoemde argument (bereiknaam) Values_ Entered speelt een startrol in de sheet.
Het model brengt pas een amortisatieplan in beeld op het moment dat alle benodigde invoer is ingevuld en de benoemde functie
Value_Entered een uitkomst geeft van '1' (= waar):
=ALS(sheet3!Loan_Amount*sheet3!Interest_Rate*sheet3!Loan_Years*sheet3!Loan_Start>0;1;0)
Dit benoemde argument in ook terug te vinden via de menuoptie Invoegen – Naam definiëren.
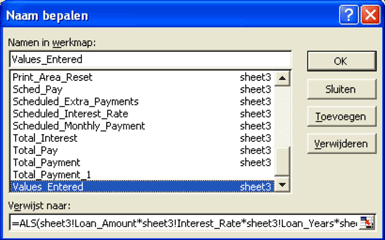
Hieruit blijkt ook dat het model werkt met nogal wat benoemde bereiken.
De in cel $D$7 opgenomen intrestvoet heeft bijvoorbeeld de naam 'Intrest-Rate' meegekregen.
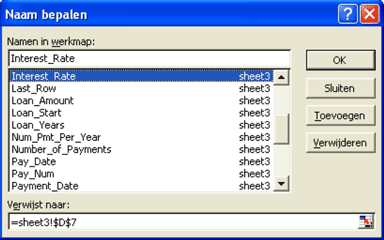
De kolommen in het model spreken verder redelijk voor zich.
In kolom B onder het kopje 'Payment Date' staan de betaaldata aangegeven.
De kolommen C (Beginning Balance) en I (Ending Balance) hangen nauw samen en geven respectievelijk het begin- en eindsaldo voor en na de betreffende termijnbetaling.
In de kolom D (Scheduled Payment) staat de annuïteit per kwartaal opgenomen. Kolom F (Total Payment) is gelijk aan kolom D, zolang er geen tussentijdse (flexibele) extra aflossing plaatsvindt in kolom E (Extra Payment).
In de kolommen G en H zijn per termijn de aflossings- en de rentebestanddelen weergegeven.
Tot slot staan in het bereik H6:H10 samenvattinggegevens opgenomen. De totale intrestkosten bedragen bijvoorbeeld € 11.736,53 (H10).
Resultaat_2
Het model biedt bovendien de mogelijkheid om eenmalig vooraf en gedurende de rit nog extra af te lossen.
Om dit te tonen hebben we in de bestaande berekening handmatig drie extra jaarlijkse aflossingen ingevoerd per 1 oktober 2008
(E20), 2009 (E24) en 2010 (E28).
We zien dat hierdoor de totale rentekosten dalen in H10.




