Introductie
Het model van Baumol werkt goed zolang er sprake is van een constante netto-uitstroom van middelen. Maar dat blijkt in de praktijk vaker niet
dan wel het geval. Op bepaalde dagen zal bijvoorbeeld sprake zijn van ontvangsten van debiteuren, terwijl op andere dagen
juist sprake zal zijn van een uitgaande kasstroom in verband met betaling aan crediteuren.
Miller en Orr hebben bekeken hoe een onderneming om moet gaan met moeilijk voorspelbare dagelijks wisselende geldstromen.
In het Model van Miller en Orr mogen de cashflows gaan tot een via het model te berekenen boven- (H) en ondergrens (L).
Bij het bereiken van de bovengrens belegt de onderneming de (overtollige) middelen tot een via het model te berekenen spilniveau
(Z). Bij het bereiken van de ondergrens (L) worden middelen aangevuld c.q. vrijgemaakt tot het spilniveau (Z). Tussen de hoogste
(H) en de laagste (L) grens mag de dagelijkse cashflow vrij schommelen.
De afstand tussen de hoogste (H) en de laagste (L) grens wordt in het model bepaald door de volgende factoren:
- de dagelijkse cashflowschommelingen: hoe groter de schommelingen hoe verder de grenzen van elkaar afliggen;
- de transactiekosten in verband met het aanvullen en beleggen: hoe hoger de transactiekosten hoe verder de grenzen van elkaar afliggen;
- de intrestkosten (opportunity-costs): hoe hoger de intrestkosten hoe dichter de grenzen bij elkaar liggen.
De vergelijkingen en variabelen
De volgende vergelijkingen en variabelen zijn van toepassing binnen het model:
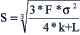 |
(I) |
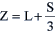 |
(II) |
| H = L + S |
(III) |
daarbij hebben de variabelen de volgende betekenis:
| H |
= |
de hoogste (=kritische) liquiditeitsvoorraad; |
| L |
= |
de gewenste en tevens laagste (=kritische) liquiditeitsvoorraad; |
| S |
= |
de spreiding tussen de hoogste H en de laagste liquiditeitsvoorraad S = (H)-(L); |
| Z |
= |
de spillijn waar naar toegewerkt wordt bij het bereiken van L (d.w.z. opwaarts aanvullen tot niveau Z) of H (d.w.z. neerwaarts
beleggen of vastzetten tot niveau Z);
|
| F |
= |
vaste transactiekosten per aanvulling (bij bereiken van Z) of belegging (bij bereiken van H); |
| σ2 |
= |
de variantie van de netto dagelijkse cashflows over een afgelopen periode; |
| σ |
= |
de standaarddeviatie van de netto dagelijkse cashflows over een afgelopen periode; |
| k |
= |
de opportunity costs in de vorm van het verschil tussen het rendement op alternatieve belegging en het rendement op liquide
middelen.
|
Doel van deze tool
Over het eerste halfjaar van 2007 geven de dagelijkse cashflows (zowel positief als negatief!) van het bedrijf C.A.S.H. het
beeld te zien in kolom H van het werkblad Cashflows voorbeeld.
In combinatie met het beginsaldo op 1 januari 2007 (F2) zijn de dagelijkse eindsaldi in kolom G weergegeven. Uit praktische overwegingen hebben we de cashflow en saldi alleen over de eerste 30 dagen weergegeven. Het patroon
voor de saldi en de cashflow over een het eerste halfjaar (periode van 182 dagen) ziet er – dit maal compleet – als in het
werkblad Grafische weergave saldi en cashflow voorbeeld.
De inkomende en uitgaande cashflow schommelt globaal tussen de grenzen van plus en minus € 1.500, de saldi tussen de grenzen
van plus € 3.000 en minus € 2.000.
In te vullen velden
Om tot kostenminimalisatie te komen vult bedrijf C.A.S.H het Miller-Orr-model (zie: het werkblad Miller-Orr-model) in:
De cijfers en formules zijn daarbij als volgt ingevoerd en berekend:
| B2 |
De standaarddeviatie van de cashflows over het eerste halfjaar: sigma |
=STDEVP(H2:H182) |
| B3 |
Gewenste minimumpositie L |
zelf in te vullen |
| B4 |
Transactiekosten F |
zelf in te vullen |
| B5 |
Dagelijkse intrestkosten k (herleiden naar dagbasis, uitgegaan van 10% per jaar) |
zelf in te vullen
=0,1^1/365 |
| B7 |
Verschil hoogste en laagste grens: S |
=3*(((3/4)*B4*B2^2)/B5)^(1/3) |
| B8 |
Hoogste kritische grens: H |
=B3+B7 |
| B9 |
Laagste kritische grens: L |
=B3 |
| B10 |
Spillijn: Z |
=B9+B7/3 |
Resultaten
Na de berekening van het model gaat het bedrijf C.A.S.H over tot implementatie voor het tweede halfjaar 2007.
Na afloop van het tweede halfjaar ziet het beeld van de dagelijkse netto cashflows in kolom P er als in het werkblad Cashflows voorbeeld na implementatie model.
In combinatie met het beginsaldo (dat we voor het gemak maar weer op € 5.000 (N2) hebben gesteld) zijn de dagelijkse ongecorrigeerde eindsaldi in kolom O weergegeven. Hierbij is nog geen rekening gehouden met de in het model (B7:B10) berekende grenzen.
Als we dat wel doen en de uitkomsten van het Miller-Orr-model volgen, dan ontstaan de gecorrigeerde saldi, zoals weergeven
in kolom Q van het werkblad Cashflows voorbeeld na implementatie model. Daarbij hebben we als volgt gebruikgemaakt van de ALS-functie
(als voorbeeld voor cel Q3):
=ALS(EN(Q2+P3>$B$9;Q2+P3<$B$8);Q2+P3;$B$10)
ofwel uitgedrukt in kritische grensbedragen:
=ALS(EN(Q2+P3>1.000;Q2+P3<9.726);Q2+P3;3.909)
Hierdoor wordt bij overschrijding van de grenzen (H = € 9.726 en L = € 1.000) de waarde gelijk aan de spilwaarde (= € 3.909).
Uit praktische overwegingen hebben we de cashflow en de saldi alleen weer voor de eerste 30 dagen weergegeven. Het patroon
voor de saldi en de cashflow ziet er compleet als in het werkblad Grafische weergave saldi en cashflow voorbeeld na implementatie
model.
Het gecorrigeerde saldo blijft binnen de H- en de L-grens en keert bij overschrijding terug naar de Z-waarde (=B10 = € 3.909).
Dat blijkt in de tweede halfjaarlijkse periode (Q2:Q182) precies tien maal te gebeuren:
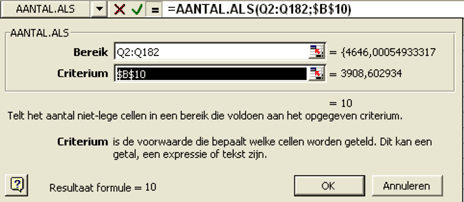
Natuurlijk zijn we erg benieuwd naar het geminimaliseerde kostenniveau.
Dit bedraagt voor de gecorrigeerde saldi en bij het 10 maal uitvoeren van een transactie:
(10*F) + (182/365)*(Gemiddeld gecorrigeerd saldo)*10% =
(10*€ 10) + 0,5*€4.880*0,1 = € 100 + € 244 = € 344
Ter overweging en zonder het verder uit te rekenen:
Dit ligt in ieder geval beneden het niveau waarbij geen correctie plaatsvindt, zeker als we de roodstand (zie lijn voor negatieve
ongecorrigeerde saldi) er bij betrekken. Hiervoor geldt altijd een aanzienlijk hoger percentage dan de 10% waar we standaard
mee rekenen binnen de gecorrigeerde kolom.
Conclusie
Het Miller-Orr-Model blijkt in de praktijk een handig hulpmiddel om de uiterste onder- en bovengrens te bepalen bij het innemen
van kasposities, zeker als de inkomende en uitgaande stromen een grillig verloop in de tijd hebben. Daarbij wordt gebruikgemaakt
van historische patronen. Het qua opzet veel eenvoudiger Baumol-model leent zich voor het optimaliseren van kasposities bij organisaties met een stabiel netto-uitgavenpatroon dat periodiek aanvulling
behoeft.
Tips & Trucs
Het vullen van een bereik met Aselecte getallen
In het voorgaande hebben we bij de vulling van de Netto-Cashflow-kolommen (H2:H182 en P2:P182) gebruikgemaakt van het Excel-onderdeel Gegevensanalyse (menu Extra – Gegevensanalyse – Aselecte getallen).
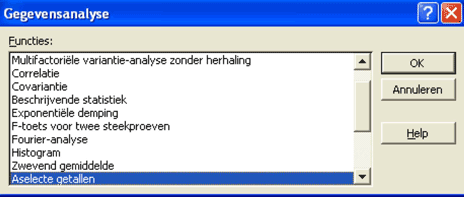
Als we een bereik willen vullen met een reeks aselecte getallen, kiezen we voor de optie Uniforme verdeling.
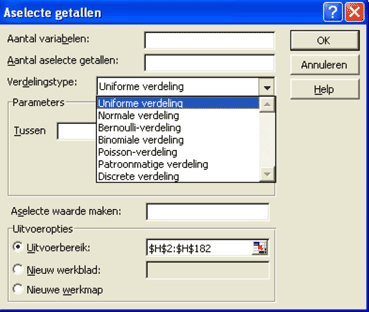
Hierna geven we de grenzen aan in de velden Tussen en en.
In ons voorbeeld hebben we vrij willekeurig gekozen voor de (saldi)grenzen - € 1.500 en € 1.500. Variabelen worden dan met
een gelijke kans getrokken uit alle waarden in het aangegeven bereik.
Na het drukken op de knop OK vult het bereik zich met aselecte getallen.
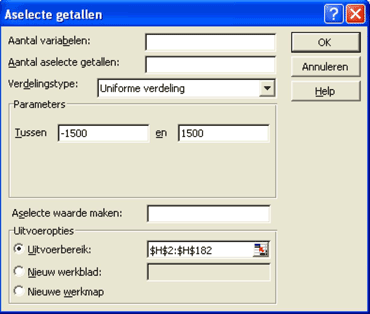
Daarnaast kan met het invoerveld Aantal variabelen worden aangegeven hoeveel kolommen met waarden in de uitvoertabel moeten worden opgenomen. Als het aantal variabelen niet
wordt opgegeven, worden alle kolommen in het uitvoerbereik gevuld.
In het veld Aantal aselecte getallen kan tot slot worden opgenomen hoeveel gegevenspunten moeten worden weergegeven. Elk gegevenspunt wordt in een rij in de uitvoertabel
geplaatst. Als het aantal aselecte getallen niet wordt opgegeven, worden alle rijen in het uitvoerbereik gevuld.