De netto contante waarde-methode in Excel
Samenvatting
De netto contante waarde-methode neemt de netto contante waarde als maatstaf voor het vergelijken van voordelen. Hoe u in Excel deze methode kunt toepassen, leest u in dit artikel. U treft allereerst een uitleg aan van het begrip, het is mogelijk om direct bij de uitleg het desbetreffende werkblad in Excel te downloaden. Vervolgens volgt een uitleg van de functie HW – huidige waarde. De uitleg is gelardeerd met diverse voorbeelden. Het artikel eindigt met een uitgebreide behandeling van de functie NHW – netto huidige waarde. Ook deze uitleg is voorzien van diverse voorbeelden. Daarnaast is een stappenplan opgenomen van het werkblad Uitleg functies HW, NHW, NHW2, TW, BET.
Wat behelst de netto contante waarde-methode?
Deze wijze van investeringsberekening neemt de netto contante waarde van investeringen als maatstaf voor het vergelijken van de (financiële) voordelen. Bij deze methode worden alle kasstromen die samenhangen met een investeringsproject terug gedisconteerd naar het begin van de gebruiksperiode of vergelijkingsperiode van de investeringsobjecten (tijdstip t0).
De netto contante waarde van een investering is het verschil
- tussen de optelling van alle investeringsgerelateerde inkomsten
(inclusief de eventuele gedisconteerde opbrengst uit liquidatie) gedisconteerd naar tijdstip t0
- en de optelling van alle investeringsgerelateerde uitgaven
(inclusief te disconteren aanschafwaarden) gedisconteerd naar tijdstip t0.
C0 = Ci - Cu = I0 + Σ Ki1-n - Σ Ku1-n + Rn
C0 = netto contante waarde (NCW)
Ci = gedisconteerde inkomsten over totale investeringslooptijd
Cu = gedisconteerde uitgaven over totale investeringslooptijd
I0 = initiële investering (uitgave) aan begin investeringsperiode
Σ Ki1-n - Σ Ku1-n = som van gedisconteerde exploitatiekasstroom (inkomsten en uitgaven) periode 1 tot en met n
Rn = gedisconteerde restwaarde (ofwel liquidatieopbrengst) aan einde investeringsperiode (jaar n)
Wanneer de (financiële) voordelen van één losstaand investeringsproject moeten worden beoordeeld, dan kan de netto contante waarde-methode worden gebruikt (zie het werkblad Berekening netto contante waarde voor één project – voorbeeld 1).
Wanneer de netto contante waarde als resultaat van de berekening groter is dan of op zijn minst gelijk is aan nul, dan kan de investering vanuit financieel oogpunt positief worden beoordeeld. In dat geval is de contante (of huidige) waarde van alle inkomsten groter dan de contante waarde van alle uitgaven die met het investeringsproject samenhangen.
De netto contante waarde-methode kan ook worden gebruikt om twee (of meer) alternatieve investeringsprojecten met elkaar te vergelijken (zie het werkblad Berekening netto contante waarde voor twee alternatieve investeringsprojecten – voorbeeld 1).
Na het maken van de berekeningen kunnen de netto contante waarden van de alternatieven worden vergeleken. Het alternatief dat de grootste positieve netto contante waarde heeft, heeft dan vanuit financieel oogpunt in principe de voorkeur (afgezien van eventuele andere overwegingen, bijvoorbeeld milieubelasting).
Zoals blijkt uit de hierna volgende voorbeelden, hebben de kasstromen in de diverse perioden een verschillende omvang. Dit betekent dat de kasstroom van elke periode (als som van inkomsten minus uitgaven in de betreffende periode) dient te worden gedisconteerd met de betreffende disconteringsfactor voor diezelfde periode.
NCW = I0 + ((i1 - u1) / q1) + ((i2 - u2) / q2) + ..... + ((in - un) / qn) + (Rn / qn)
Een eventuele liquidatieopbrengst (restwaarde, Rn) van het investeringsobject, die aan het eind van de gebruiksperiode als inkomsten naar het bedrijf terugvloeit, wordt gedisconteerd met de overeenkomstige disconteringsfactor en wordt in het laatste jaar ofwel als inkomsten apart opgevoerd (zoals in de formule hierboven) of wordt meegenomen bij de kasstroom van het investeringsproject in het laatste jaar.
Slechts in uitzonderlijke gevallen zijn de kasstromen in de betreffende perioden altijd gelijk. In die gevallen hoeven de kasstromen per periode niet apart of gedifferentieerd te worden gedisconteerd. De netto contante waarde kan dan worden vastgesteld door het toepassen van de factor contante waarde (zie Achtergrondinformatie Dynamische investeringsberekeningen).
c0 = e x ((qn - 1) / (qn x (q - 1))) - i0
C0 = netto contante waarde (NCW)
e = jaarlijks (gelijkblijvende) kasstroom (inkomsten - uitgaven)
I0 = initiële investering (aanschafwaarde)
Tips Financiële functies in Excel
Tussen de ruim 300 functies van Excel vindt u ook de financiële functies. Veel gebruikers van Excel kennen deze financiële functies nauwelijks. Vijf financiële functies van Excel maken het beoordelen van investeringen gemakkelijker.
Deze functies zijn:
- HW – huidige waarde;
- NHW – netto huidige waarde (ofwel netto contante waarde);
- NHW2 – netto huidige waarde 2;
- TW – toekomstige waarde;
- BET – betaling.
De beschreven Excel-functies worden in de voorbeeldwerkbladen bij het onderdeel De functie HW gebruikt.
Wat berekent de functie HW – huidige waarde?
Deze functie berekent de contante waarde van betalingen (inkomsten en/of uitgaven). De huidige waarde is het totale bedrag dat een reeks toekomstige periodieke betalingen op dit moment waard is.
Deze functie ziet er als volgt uit:
HW (Rente, Aantal_termijnen, Bet, tw, type_getal)
De verplichte argumenten van deze functie zijn:
Checklist Argumenten functie HW
- Rente: dit is het rentepercentage per termijn. Let op: als u maanden als termijn gebruikt, moet u een rentepercentage dat betrekking heeft op een jaar ook vertalen naar een maandrente (door deze te delen door 12).
- Aantal termijnen: hier geeft u het totale aantal termijnen aan.
- Bet: geeft het bedrag aan dat elke periode betaald wordt. Dit bedrag is voor elke periode gelijk.
De optionele argumenten die gebruikt kunnen worden, zijn:
- Tw: dit is de toekomstige waarde. Als u Tw weglaat, wordt uitgegaan van de waarde nul. Als u het argument Bet gebruikt, kunt u dit argument weglaten.
- Type_getal: u geeft 1 aan als de betalingen telkens aan het begin van een periode voldaan worden. Als u 0 aangeeft (of dit argument leeg laat) betekent dit dat de betalingen telkens aan het eind van een periode voldaan worden.
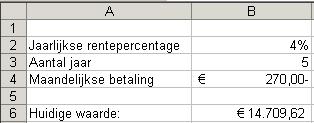
Voor enkele rekenvoorbeelden van wel of geen maandelijkse inleg klik hier. X U wilt weten wat de huidige waarde is van een maandelijkse inleg van 270 euro op een spaarrekening tegen 4%, als u dit vijf
jaar doet.
In cel B6 vindt u de volgende formule:
=HW(B2/12;B3*12;B4;0;1). In dit voorbeeld zijn we ervan uitgegaan dat de inleg telkens aan het begin van een maand plaatsvindt. Omdat sprake is van
maandelijkse betalingen moet de gegeven jaarrente worden aangepast naar een maandrente (4%/12 ofwel B2/12) en moet het aantal
termijnen in jaren worden aangepast naar een aantal termijnen in maanden (5 x 12 ofwel B3*12). Op deze wijze zijn alle gebruikte
gegevens intern consistent, namelijk gebaseerd op maanden.
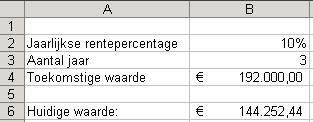
U verwacht over drie jaar een positieve cashflow te ontvangen van € 192.000. Uitgaande van een rente van 10% is deze cashflow
op dit moment € 144.252,44 waard. Dit berekent u als volgt:
De formule in cel B6 ziet er als volgt uit: =-HW(B2;B3;0;B4). In dit voorbeeld is geen sprake van maandelijkse betalingen, maar van een eenmalige betaling op een moment in de toekomst.
In dat geval wordt niet het argument Bet gebruikt, maar het argument tw. Het argument Type-getal is in dit voorbeeld weggelaten.
Dit betekent dat ervan wordt uitgegaan dat de ontvangst van het bedrag van € 192.000 aan het einde van jaar drie zal plaatsvinden.
Voorbeeld Maandelijkse inleg
Uitwerking:
Voorbeeld Geen maandelijkse betaling
Wat berekent de functie NHW – netto huidige waarde?
Deze functie berekent de netto huidige waarde (ofwel de netto contante waarde) van een investering met een reeks kasstromen, bestaande uit toekomstige uitgaven (negatieve waarden) en inkomsten (positieve waarden).
Excel gaat ervan uit dat de cashflows ontvangen worden aan het eind van de periodes. Als de eerste cashflow aan het begin van de eerste termijn plaatsvindt (ofwel op tijdstip t0), moet u deze waarde apart bij de berekening van de NHW van de overige cashflows optellen en NIET in de functie als waardeargument meenemen.
De functie ziet er als volgt uit:
=NHW(rente; waarde1; waarde2;...; waarde29)
De (verplichte) argumenten van deze functie zijn:
Checklist Argumenten NHW – netto huidige waarde
- Rente: dit is het rentepercentage dat als disconteringsvoet moet worden toegepast op de cashflows. Bij een investeringscalculatie vertegenwoordigt dit rentepercentage de vermogenskosten van het bedrijf.
- Waarde1, waarde2 (tot en met maximaal waarde29) zijn de kasstromen die elke periode plaatsvinden. In tegenstelling tot bij de functie HW mogen de kasstromen bij gebruik van de functie NHW per periode verschillen. De gebruikte waarden kunnen zowel negatieve waarden (als per saldo in een periode sprake is van uitgaven) als positieve waarden (als per saldo in een periode sprake is van inkomsten) zijn. Excel gebruikt de volgorde van deze waarden om de volgorde van de cashflows te bepalen. Met andere woorden, Excel veronderstelt dat waarde 1 valt aan het einde van periode 1, waarde 2 aan het einde van periode 2, enzovoort. De cashflows moeten dus in de juiste volgorde aangegeven worden.
Zorg dat de termijn die wordt gehanteerd voor de rente en de waarden overeenkomen, dat wil zeggen bij bijvoorbeeld maandelijkse kasstromen hoort een maandelijks rentepercentage, bij jaarlijkse kasstromen hoort een jaarlijks rentepercentage, enzovoort.
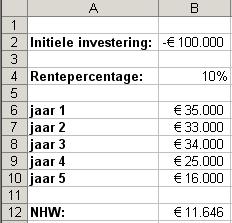
Voor een voorbeeld van de functie NHW klik hier. X Een investering van € 100.000 genereert over de komende vijf jaar de onderstaande cashflows. De vermogenskosten van het betreffende
bedrijf zijn 10% per jaar. Wat is de netto contante waarde van deze investering?
De berekening van de netto huidige waarde in cel B12, met een rente van 10% ziet er als volgt uit: =NHW(B4;B6:B10)+B2Voorbeeld Netto huidige waarde
In de NHW-functie gaat Excel ervan uit dat de periodes gelijk zijn, bijvoorbeeld altijd maanden of jaren waarbij de kasstroom telkens aan het einde van elke maand respectievelijk elk jaar valt. In de praktijk hoeft dit niet altijd het geval te zijn. Om de netto huidige waarde van een investering met onregelmatige cashflows te berekenen, beschikt Excel over de functie NWH2.
Wat berekent de functie NHW2?
Deze functie is geen standaardfunctie van Excel, maar opgenomen in de zogenoemde Analysis ToolPack. Om gebruik te kunnen maken van deze functie dient u bij de menu-optie Extra – Invoegtoepassingen het vinkje bij de toepassing Analysis ToolPack aan te zetten.
De syntaxis van deze functie ziet er als volgt uit:
NHW2 (rente, waarden, datums)
De (verplichte) argumenten van deze functie zijn:
Checklist Argumenten NHW2
- Rente: dit is het rentepercentage dat als disconteringsvoet moet worden toegepast op de cashflows en vertegenwoordigt de vermogenskosten van de organisatie.
- Waarden: dit zijn de inkomende (positief) of de uitgaande (negatieve) cashflows.
- Datums: dit zijn de datums waarop de cashflows gegenereerd worden.
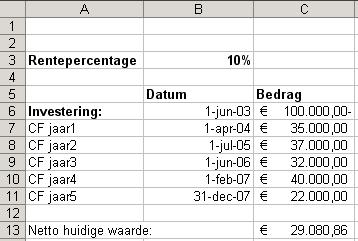
Voor een voorbeeld van de functie NHW2 klik hier. X Een investering van € 100.000 op 1 juni 2003 genereert over vijf jaar de volgende cashflows: De berekening van de netto contante waarde, rekening houdend met de datums waarop de cashflows binnenkomen, ziet er als volgt
uit:
=NHW2(B3;C6:C11;B6:B11) De omvang van het celbereik dat verwijst naar de cashflows moet even groot zijn als de omvang van het celbereik dat verwijst
naar de datums, anders levert de functie een foutmelding op.
Voorbeeld NHW2
Wat berekent de functie TW – toekomstige waarde?
Deze functie berekent de toekomstige waarde van een lening of een investering als we het rentepercentage kennen, het aantal termijnen en de (gelijkblijvende) betaling per termijn.
De functie ziet er als volgt uit:
=TW(rente; aantal_termijnen; betaling; huidige_waarde, type_getal)
De argumenten hebben dezelfde betekenis als bij de checklist functie HW (zie hiervoor).
Voor een voorbeeld van de functie TW klik hier. X Als u tien jaar lang elke maand € 200,00 op een spaarrekening zet tegen 4% rente per jaar, hebt u na tien jaar € 29.548,13
gespaard. Dit berekent u als volgt:
De formule in cel B6 ziet er als volgt uit: =TW(B2/12;B3*12;B4;0;1) Let op: we zijn ervan uitgegaan dat de betalingen in het begin van de maand plaatsvinden (type_getal=1).Voorbeeld Functie TW

Misschien vraagt u uzelf af hoeveel u per maand moet sparen als u na tien jaar € 20.000 wilt hebben. Dit berekent u met behulp van de Excel-functionaliteit Doelzoeken.
Stappenplan Werkblad Uitleg financiële functies
Stap 1. Open het werkblad Uitleg financiële functies HW, NHW, NHW2, TW, BET en selecteer het werkblad TW.
Stap 2. Selecteer cel B6.
Stap 3. Ga naar de menuoptie Extra – Doelzoeken.
Stap 4. Verander de instellingen zoals in dit voorbeeld.
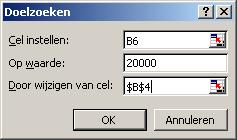
Stap 5. Klik op OK.
Zoals u ziet, heeft Excel een oplossing voor u gevonden:
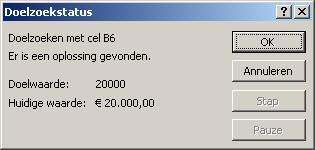
U moet dan € 135,37 per maand sparen.
Wat berekent de functie BET – betaling?
Deze functie berekent het bedrag dat periodiek betaald moet worden op een lening uitgaande van vaste (gelijkblijvende) periodieke betalingen en een vast rentepercentage voor de hele periode. Deze betaling vertegenwoordigt het periodieke bedrag aan rente en aflossing.
De functie ziet er als volgt uit:
=BET(Rente; Aantal_termijnen; Huidige_waarde; Toekomstige_waarde; Type_getal)
De verplichte argumenten van deze functie zijn:
Checklist Argumenten BET
- Rente: dit is het rentepercentage per termijn. Let op: als u maanden als termijn gebruikt, moet u een rentepercentage dat betrekking heeft op een jaar ook vertalen naar een maandrente (door deze te delen door 12).
- Aantal termijnen: hier geeft u aan het totale aantal termijnen (periodes) aan.
- Huidige_waarde: geeft het bedrag aan dat als lening is verstrekt aan het begin van de eerste periode. Dit wordt ook wel de hoofdsom van de lening genoemd. Het is het totaalbedrag dat alle toekomstige betalingen op dit moment waard zijn.
De optionele argumenten die gebruikt kunnen worden zijn:
- Toekomstige_waarde: dit is de toekomstige waarde, ofwel het saldo dat u wilt bereiken als de laatste betaling is verricht. Als u Tw weglaat, wordt uitgegaan van de waarde nul (immers, de toekomstige waarde van bijvoorbeeld een volledig afgeloste lening is 0).
- Type_getal: u geeft 1 aan als de betalingen telkens aan het begin van een periode voldaan worden. Als u 0 aangeeft (of dit argument leeg laat) betekent dit dat de betalingen telkens aan het eind van een periode voldaan worden.
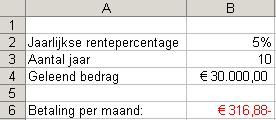
Voor een voorbeeld van de functie BET klik hier. X U leent vandaag € 30.000 voor een periode van tien jaar tegen een rente van 5% per jaar. Hoeveel moet u dan per maand betalen
om de lening volledig af te lossen?
In cel B6 vindt u de volgende formule:
=BET(B2/12;B3*12;B4;0;1) Merk op dat we er hier van uitgaan dat de betaling aan het begin van elke maand plaatsvindt.Voorbeeld Functie BET
Conclusie
De Excel-functies HW, NHW, NHW2, TW en BET maken het beoordelen van investeringen gemakkelijker. Alle vijf de Excel-functies zijn uitgewerkt aan de hand van voorbeelden. De functie NHW2 is geen standaardfunctie van Excel maar is opgenomen in de zogenoemde Analysis ToolPack. Door bij de menu-optie Extra – Invoegingstoepassingen het vinkje bij Analysus ToolPack aan te zetten kunt u gebruikmaken van deze functionaliteit. Het stappenplan Uitleg financiële functies leidt u door de Excel-functionaliteit Doelzoeken om bijvoorbeeld te berekenen hoeveel u per maand moet sparen als u na tien jaar een bepaald bedrag wilt hebben.
Direct aan de slag met Investeringsselecties: werkbladen in Excel!
Artikel als PDF downloaden
Vul hieronder uw e-mailadres in om de PDF-versie van dit artikel te ontvangen:
Personeelsmanagement

Heeft u ook een verantwoordelijkheid in personeelsmanagement? Kijk dan ook op HR Praktijk voor zekerheid over wetten en regels!
