WAKE BV vervaardigt en verkoopt twee soorten producten: A en B. Het streven van WAKE BV is gericht op een maximale dekkingsbijdrage per week. De dekkingsbijdrage van A respectievelijk B bedraagt € 2.500 en € 3.000 per 1000 eenheden. Per week heeft WAKE BV de beschikking over 2700 arbeidsuren en 3600 machine-uren. Per 1000 eenheden A zijn 27 arbeids- en 24 machine-uren vereist, voor B respectievelijk 15 arbeids- en 40 machine-uren.

Als we de meest relevante gegevens op een rijtje zetten, krijgen we samengevat:

Tot slot dient WAKE BV wekelijks contractueel ten minste 30.000 stuks A en 30.000 stuks B te leveren. De totale constante kosten bedragen € 190.000 per week.

Voor de modelvorming stellen we:

X = het aantal te produceren duizendtallen van A
Y = het aantal te produceren duizendtallen van B

De vier restricties luiden dan:

27 X + 15 Y ≤ 2.700 (arbeidsuren)

24 X + 40 Y ≤ 3.600 (machine-uren)

X ≥ 30 (hoeveelheid A)

Y ≥ 30 (hoeveelheid B)

en de doelfunctie:

D(X,Y) = 2.500 X + 3.000 Y

De handmatige oplossing bij twee variabelen

Als we het probleem grafisch weergeven, krijgen we:

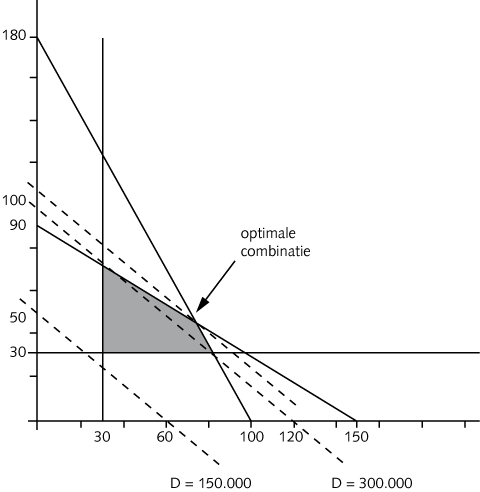
We zien dat:

• de eerste restrictie van het punt (X, Y) = (0,180) naar (X, Y) = (100,0) loopt;
• de tweede restrictie van het punt (X, Y) = (0,90) naar (X, Y) = (150,0) loopt;
• de derde restrictie begint in het punt (X, Y) = (30,0) en verticaal naar boven loopt;
• de vierde restrictie begint in het punt (X, Y) = (0,30) en horizontaal loopt.

Als we de vier restricties combineren, komen we terecht in het grijs gearceerde vlak.

Het optimum bevindt zich in het punt dat het verst afgelegen is van de coördinaat (X, Y) = (0,0). We kunnen het snijpunt van de bijbehorende coördinaten berekenen door de onderliggende twee vergelijkingen (restrictie 1 en restrictie 2) met twee onbekenden (X en Y) op te lossen. Dit doen we door eerste de onbekende Y weg te werken en vervolgens X en Y te berekenen en hiervan het verschil te bepalen:

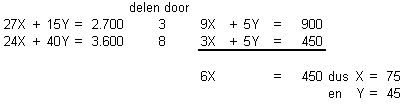
De maximale dekkingsbijdrage bedraagt dan:

D (75,45) = 2.500 × 75 + 3.000 × 45 = 322.500

Deze maximale dekkingsbijdrage ligt op een schuine ISO-lijn die alle X- en Y-punten verbindt met een gelijke dekkingsbijdrage van € 322.500. Het gevonden optimum is daarbij het enige punt waarbij nog net aan de vier restricties wordt voldaan.

Ter illustratie hiervan zijn er nog twee andere ISO-lijnen zichtbaar in de grafiek: één waarbij sprake is van een dekkingsniveau van € 150.000 en één met een dekkingsniveau van € 300.000. Merk op dat bij de lijn die aansluit op een dekkingsniveau van € 150.000 in geen van de combinaties wordt voldaan aan de gewenste productieniveaus van zowel minimaal 30.000 eenheden X als Y !

Tot slot en aansluitend op het gevonden maximum bedraagt de maximale winst:

€ 322.500 – € 190.000 = € 132.500

Voor de berekening met de Oplosser zie 'Winstmaximalisatie'.